Переступив порог двери, ведущей к чудесам...

 

Математика — это основное средство, созданное человеком для познания вселенной. Она окружена стенами, в которых иногда обнаруживаются двери. Эти двери ведут в мир чудес — войдя внутрь через одни из таких дверей, человек перестает быть хозяином положения. Перед ним открываются исключительные и блестящие возможности создания сочетаний Он оказался — в мире чисел. Не будем мешать вошедшему восторгаться столь обильно разлившимся светом.

 

Яркость света почти непереносима. Нас поддерживает увлеченная молодежь, не сознающая своей ответственности; это присуще ее возрасту; в этом ее сила и слабость; если не оказать ей сопротивления, он окутает нас туманом своих сомнений. А в том деле которое нас интересует, надо быть непреклонным и твердо знать, к чему стремишься; а мы хотим создал такой точный инструмент, с помощью которого можно будет назначать размеры. Взяв путеводный компас в руки, последуем за ним по миру чисел; а пути расходятся по разным направлениям, множатся, разветвляются, ширятся... Это может увести нас далеки от поставленной цели: мы станем жертвами законов мерностей, присущих самим числам. Великие теоретики архитектуры эпохи Возрождения пошли по этим заманчивым путям. Я никогда не признавал то к чему они пришли, — архитектуру этой и последую щей эпохи; сначала я просто почувствовал свое несогласие с этой архитектурой, но долгое время не моя понять причины этого чувства. То была «бумажная архитектура»; с помощью циркуля строили звездообразные композиции. Геометры эпохи Возрождения создавали икосаэдры и додекаэдры в виде звезд, направляя все свои мысли на философское обоснования такого зодчества, полностью отрешаясь от конкретных условий зрительного восприятия. Вся система строилась без всякого учета зрительного восприятия; те, кто сегодня созерцает их произведения, не в со стоянии понять намерений, которыми они руководствовались при их создании. Человек, сопоставляя разные возможности с закрытыми глазами, рассуждает отвлеченно. Однако он строит с открытыми глазами; он выявляет свою точку зрения. Его глаза (а их всего два, а не десять, не сто и не тысяча) расположены на лицевой, передней, части головы; они смотрят прямо перед собой и не видят того, что находится сбоку и сзади; они поэтому не в состоянии оценить все разнообразие различных сочетаний, образующихся по контуру очертаний умозрительно построенных многоугольных композиций. Архитектуру мы воспринимаем открытыми глазами, поворачивая голову и переходя с одного места на другое. Архитектура — не феномен, воспринимаемый сразу; она создается из ряда образов, последовательно накладывающихся один на другой во времени и пространстве, подобно музыке. Это крайне важно и имеет, быть может, основное, даже решающее значение; звездообразные композиции эпохи Возрождения породили архитектуру эклектическую, умозрительную, воспринимаемую лишь в виде повторяющихся фрагментов, соответствующих многочисленным осям звездообразных композиций. Зрение человека — это не зрение мухи, глаза которой представляют собой многогранники. Глаза человека расположены на высоте в среднем 1,6 м от земли. Таков инструмент, которым мы располагаем для восприятия архитектуры. Поле зрения человека весьма ограниченного размера; в еще большей степени оно ограничено сознанием, которое, вслед за зрительным аппаратом, воспринимает, оценивает и измеряет лишь то, на что ему хватает времени.

 

Фенелон, живший спустя два столетия после гуманистов эпохи Возрождения, во времена поистине гибельные для архитектуры, в период глубокого извращения «классики», сказал: «Остерегайтесь дьявольских чар и привлекательности геометрии». 

 

Подобная же проблема встала в музыке, когда пытались найти наиболее точно воспроизводящий ее способ записи. Были установлены интервалы между тонами, воспринимаемые слухом, и отвечающие им числовые значения частот. «Встал вопрос о выборе из 300 различаемых слухом звуков октавы, об определении практически пригодной гаммы, состоящей из ограниченного числа звуковых тонов. Мне хотелось бы, чтобы читатель понял всю серьезность вопроса: от его решения зависело, в известной мере, музыкальное творчество на тысячи лет, если даже не навеки» (Анри Мартен. Математика и музыка, 1948.).

 

«Музыка — это занятие математикой в скрытом виде, а тот, кто ею занимается, не подозревает даже, что оперирует числами» (Лейбниц).

 

«Играющий на клавесине не сознает, что имеет дело с логарифмами» (Анри Мартен).

 

«Не музыка входит в число математических дисциплин, наоборот, естественные науки являются частью музыки, поскольку в их основе лежат пропорции, а пропорции — это порождение звучащего тела». Смыслом этого заносчивого утверждения Рамо проникнуто все наше исследование: над всем господствует, властвует музыка. Точнее говоря — гармония. Гармония, господствующая, управляющая всем, что нас окружает, — это стихийное, неизменное и настоятельное стремление, присущее человеку, одержимому возвышенной целью превратить землю в рай. Райским   на Востоке называли сад, расцвеченный всеми красками самых прекрасных цветов и растений, пылающих не только под солнечными лучами, но и в тени. Человек в состоянии мыслить и действовать только как человек (соблюдая  присущие ему масштабы) и участвовать в жизни вселенной (подчиняясь ритмам, определяющим дыхание земли). В этом созвучии и расхождении, в единстве и противоположности судеб одного (человека) и другой (вселенной) тотчас проявляются размерные величины, доступные нашему пониманию и относящиеся к одному или другому масштабу.

 

Хорошей композиции можно добиться с помощью весьма ограниченного числа элементов; нужно, однако, чтобы каждый из них обладал ярко выраженной индивидуальностью. Для написания десятков тысяч слов на пятидесяти языках достаточно 26 букв (Жорж  Садуль). На современном уровне знаний считают, что вся вселенная образована всего из 92 элементов. В арифметике используется всего 10 цифр; в музыке — семь нот. Год состоит из четырех времен года, двенадцати месяцев и из суток длительностью 24 часа. Часами, днями, месяцами и годами мы определяем планы наших деяний. Во всем проявляется сочетание космических и земных порядков. Порядок — основа жизни. Вернемся к нашей основной теме, в задачи которой входит объяснение того, как было создано новое средство для назначения размеров. 

 

На рис. 27 показано графическое построение пропорций фасада здания. Глазами этот фасад воспринимается по его форме, размерам, протяженности и высоте совершенно так же, как воспринимается живописное полотно. Процесс самого восприятия в данном случае абсолютно объективен.

 

Здесь же показана архитектурно-градостроительная композиция, состоящая из ряда крупных сооружений и вписанная в ландшафт. С первого взгляда невозможно определить закономерности композиции, так как одного фронтального восприятия недостаточно, а поскольку одно здание скрыто за другим, земная поверхность уходит вдаль.

 

В основе всех числовых значений — величина 113 — высота   до   солнечного   сплетения   человека  ростом 6  футов; произведены следующие основные действия: 

удвоение;

увеличение в отношении золотого сечения;

уменьшение в отношении золотого сечения. 

 

 

К этому мы пришли в 1948 году после семи лет теоретических  исследований  и  проверок  на  практике. Теперь любой школьник, первоклассник, сможет за пять минут научиться пользоваться Модулором; это значительно легче, чем выучить таблицу умножения. Каждой числовой величине на шкале Модулора отвечает соответствующее деление. Эти деления являются лишь вехами в общем ряду числовых величин, которые могут быть получены при пользовании Модулором  (см. таблицу). Ведь каждый интервал между смежным делением может быть также разделен по общему для всего Модулора принципу, создавая таким образом бесчисленное количество возможных сочетаний размеров.  Так, например, интервал между 13,901 и 8,591, равный 5,309, может быть в свою очередь расчленен делениями, равными 3,281—2,028—1,253—774 и т. д. Это как бы абсолютно однородная, лишенная разрывов ткань, с переплетением нитей, образующих сетку с ячейками от самых крупных до мельчайших размеров.

 

 

 

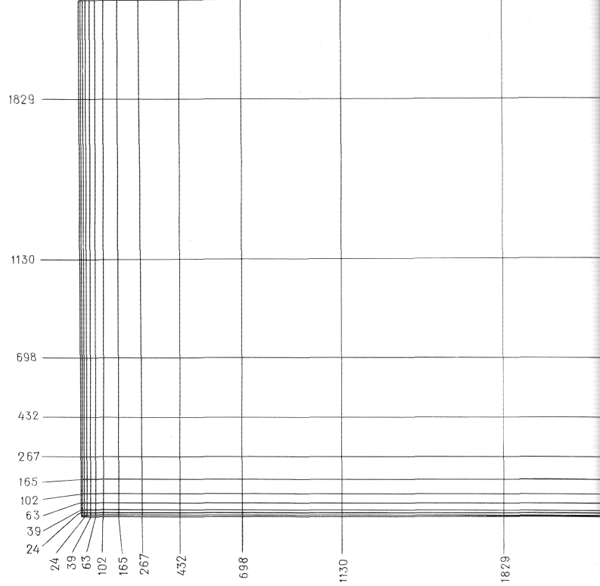
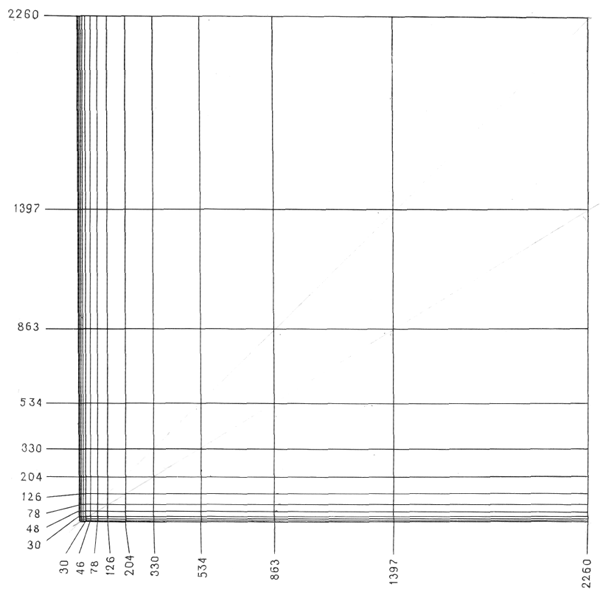
Линейные размерные величины красного и синего ряда могут образовать для каждого из рядов различные плоские фигуры, которые, начиная с квадрата, превращаются во все более вытянутые прямоугольники и в конце концов сливаются в линию. На рис. 22 показана сетка, построенная на основе красного, а на рис. 23 — на основе синего ряда.

 

 

На рис. 24 показаны совмещенные сетки красного и синего ряда, а на рис. 25 — точки пересечения сеток,

которые определяют величины, также находящиеся в отношениях золотого сечения; так:

a — основная единица;

b — удвоенная единичная величина;

c — величина в отношении золотого сечения.

 

На этих рисунках речь идет о длинах, поверхностях и объемах, которые могут быть получены на основе присущих человеческой фигуре характерных размеров. Красный ряд начинается с нуля и доведен до 1,828 м (72 дюйма); синий ряд также начинается с нуля и доведен до 2,26 м (89 дюймов). Завершается он величиной 2,26 м, которая может послужить основанием для построения единицы объема (куб со сторонами, равными 2,26 м), который, как мне кажется, можно использовать во всех случаях, связанных со строительством.

 

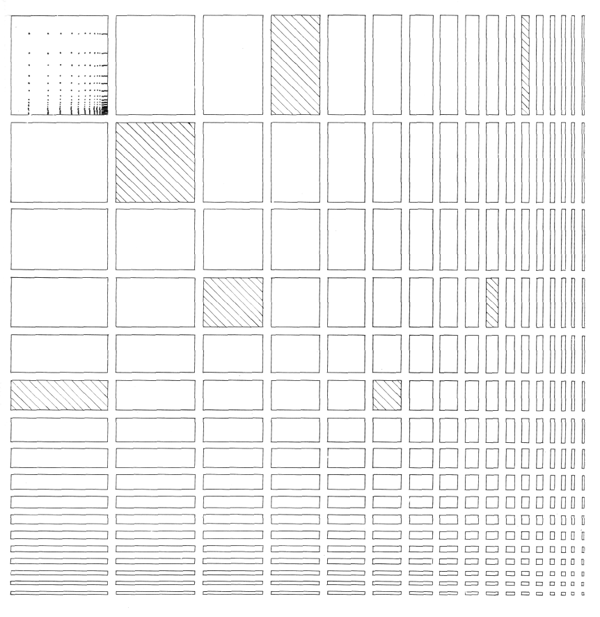
Квадрат со сторонами, равными 2,26 м, в левом верхнем углу на рис. 23 повторяет в уменьшенном масштабе построение, приведенное на рис. 25. Любая из плоских фигур на рис. 28 также может быть расчленена в таких же пропорциональных соотношениях.

 

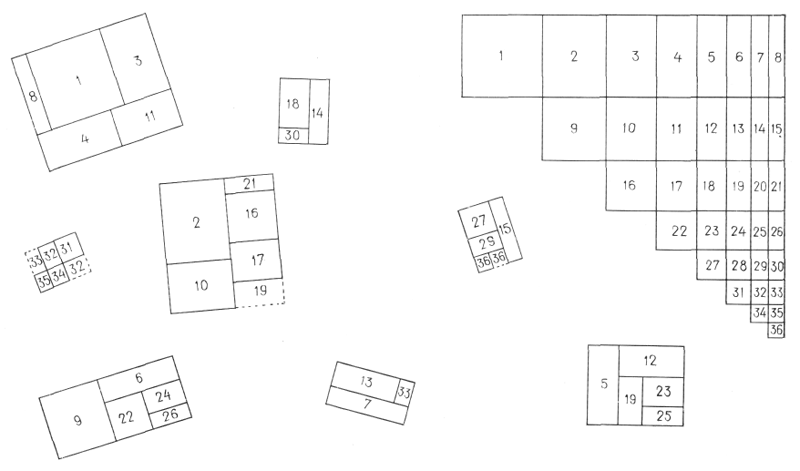
На рис. 28 заштрихованные прямоугольники показывают все разнообразие полученных форм как но размерам, так и по пропорциям. В этом можно полностью убедиться следующим образом: вырежем по уступчатой диагонали половину фигур, изображенных на рис. 28. Пронумеруем прямоугольники, чтобы их затем легче было вновь собрать*. Образуем из этих прямоугольных фигур самые разнообразные сочетания (рис. 26). Их разнообразие весьма велико. Как первое из этих сочетаний, так и все последующие оказываются прекрасными, так как образованы из элементов, подчиняющихся единой системе пропорций.

 

 

Изобретательность и вкус помогут отобрать из этих сочетаний наиболее подходящие. Могут быть созданы сочетания, отвечающие любому замыслу и конкретным условиям.

 

Итак, возможности, которые предоставляет Модулор, выявлены. С его помощью можно назначать размеры отрезков прямых линий, поверхностей и объемов. Во всех случаях эти размеры соразмерны человеческому масштабу, они обеспечивают возможность образования бесчисленного множества сочетаний, сохраняя единство при всем разнообразии; в этом заключено достоинство, которое невозможно переоценить; в этом проявление чудесных свойств чисел.

 

 

 

 

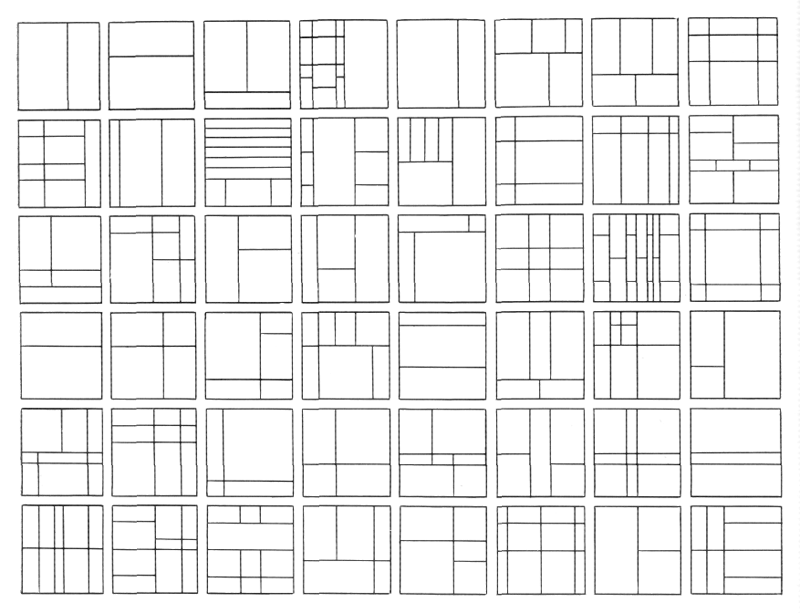
На рис. 29 показаны комбинации, названные «Игра плоскостных панелей».

 

Берем, например, квадрат и членим его, пользуясь размерными величинами Модулора. Это можно делать без конца.

 

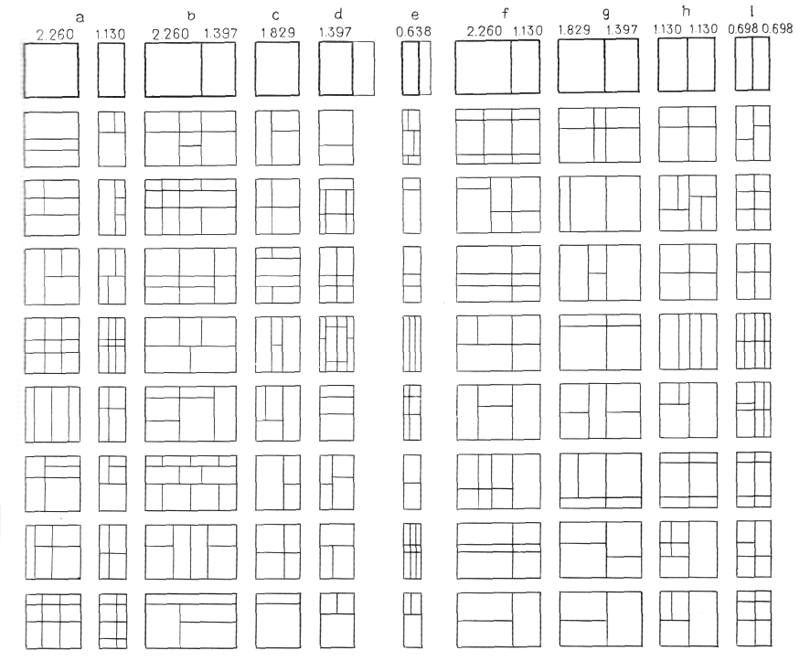
Можно было бы попытаться определить, какое из этих сочетаний наиболее удачно. На рис. 27 дан еще один пример игры по членению плоскости: а) для членения квадрата использовано пять прямой угольников разного вида, размеры которых отвечаю» Модулору. Приведено 16 квадратов с различным сочетанием этих прямоугольников; b) для членения квадрата использовано четыре вида прямоугольником размеры которых также определены по Модулору. с) членение квадрата с помощью трех видов прямоугольников с размерами по Модулору. Приведена также первая серия в 16 квадратов из всего числа возможных сочетаний. На рис. 30 показано продолжение «Игры по членению плоскости»; однако использовано членение исходного квадрата со сторонами 2,26 м (89"). Берем: а) квадрат со сторонами 2,26 м и его половину, прямоугольник 113 х 2,26 м (примеры возможных членений показаны под ними); b) прямоугольник, состоящий из квадрата  2,26 х 2,26 м (89" X 89") и прямоугольника с основанием в отношении золотого сечения, равным 1,397 м (55"); с) прямоугольник с основанием, равным одной из исходных размерных величин 1,829 м (72"); d)  прямоугольник с основанием в отношении золотого сечения к 2,26 м (89"), т. е. 1,397 м (55"); е)  прямоугольник с основанием, находящимся в отношении золотого сечения к одной из исходных размерных величин 1,13 м  (44½"), т.е. 0,698 м (27½");

f)  прямоугольник с основанием, равным сумме исходной величины 2,26 м (89") и ее половины 1,13 м (44 ½");

g)  прямоугольник с основанием, равным сумме двух из исходных размерных величин 182,9 м (72") и 1,397 м (55"); 

h) прямоугольник с основанием, равным удвоенной одной из исходных размерных величин 1,13 м (44½");

i) прямоугольник с основанием, равным удвоенной величине в отношении золотого сечения к предыдущей 0,698 м (27 1/2").

 

Получаем исключительное разнообразие гармоничных комбинаций. Число их безгранично. Остается только выбрать то или иное сочетание, отвечающее поставленной задаче.

 

Достоинство игры по членению плоскости в том, что при всей строгости, можно сказать даже при неумолимости геометрических построений, сохраняется полная свобода выбора решения, отвечающего индивидуальному вкусу. «Игры по членению плоскости», проведенные Ханнингом, обладали своеобразным характером; другого характера были упражнения, которые осуществил де Лоос 18 июля 1944 г.* Отличались от них и упражнения, проведенные Превералем в 1946 г. Эти построения могли бы служить примером графического свидетельства своеобразия художественного чутья каждого из них, психологической и физиологической реакции каждого участника этих упражнений. Ханнинг, де Лоос и Превераль были работниками мастерской на ул. Севр; выполняя одинаковые задания, каждый из них давал различные решения.

 

 

Кстати, выскажу несколько соображений по поводу примеров «Членения плоскости», предложенных Лоосом:

 

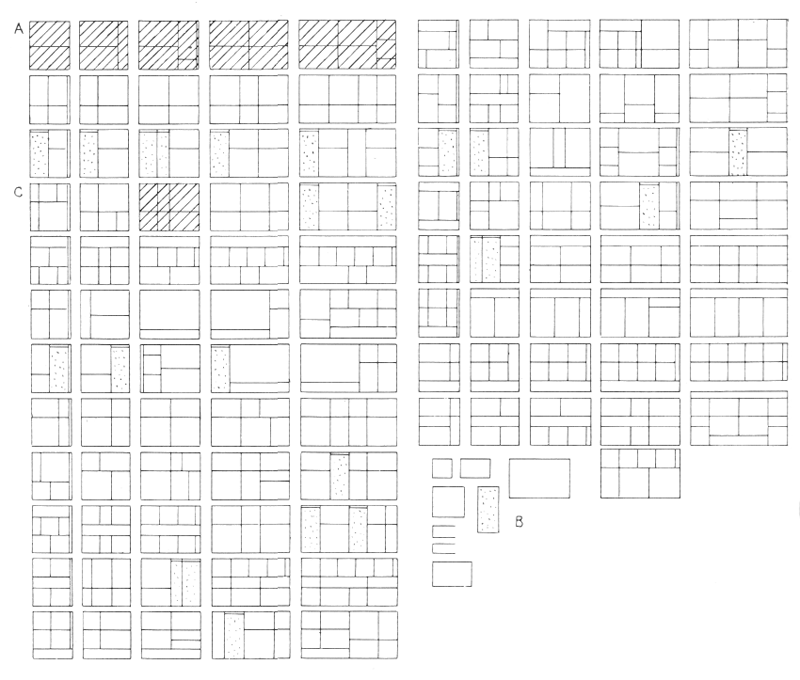
Первое задание сводилось к тому, чтобы определить пять плоскостей (рис. 31), подходящих для использования в качестве оконных проемов или столярных панелей. Был получен 101 вариант их членения, в каждом из которых использовалось пять видов прямоугольников и две узкие полоски разной ширины (В). Продолжим же наши упражнения, переступив порог «двери, ведущей в мир чудес», — поэтический символ, который я применил, говоря о тех, кто постиг все великолепие игры чисел.

 

Примечание. Прямоугольник с пунктиром высотой 2,05 м может быть использован в качестве двери; зазор, учитывая исходную высоту 2,26 м, может быть предназначен для установки осветительного устройства. Модулором предусмотрены габаритные размеры, например исходная размерная величина 2,26 м. Впредь до какого-либо нового обоснования я сохраняю уже в течение 20 лет высоту дверей от 190 до 205 см, обеспечивающую свободный проход. В этом допущено некоторое отступление, личная свободная трактовка Модулора с ограничениями и допусками.

 

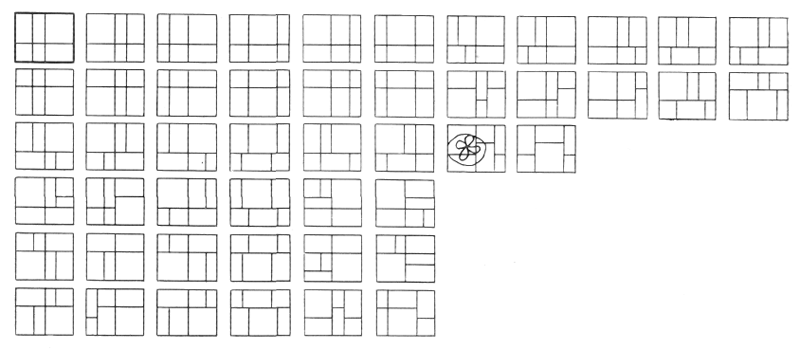
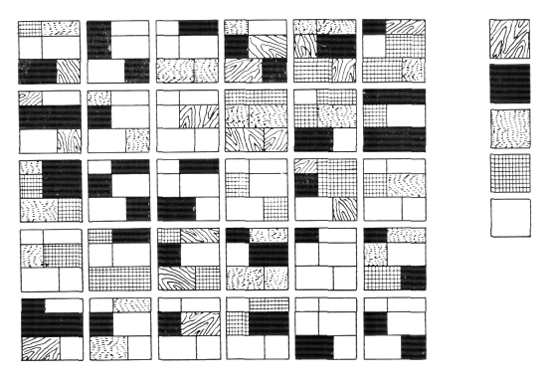
Выберем любое из 101 полученных сочетаний, например в ряду С (рис. 31). Пользуясь все теми же пятью прямоугольниками и двумя узкими полосами, мы продолжим упражнение и получим на его основе еще 48 сочетаний (рис. 32); все они гармоничны и приемлемы для архитектора.

 

Каждое из 101 сочетания, приведенного на рис. 31, может дать 48 вариантов (по примеру рис. 32); это составляет 4848 сочетаний, из числа которых каждый может выбрать любое по своему вкусу, отвечающее заданным условиям, обстоятельствам и т. д. Приведем еще одно упражнение:

 

На рис. 32 выбираем одно из сочетаний, отмеченное кружком. Решим применить в композиции пять различных материалов. На планшете появляется серия, состоящая из 30 новых сочетаний (рис. 33). Прекратим на этом нашу игру. Ведь если появится желание заняться игрой, используя Модулор, то можно посвятить этому чудесному занятию не только несколько часов, но и целые недели, даже годы. Г-н Мужо, о котором я уже говорил выше и которому я передал на сутки все материалы по Модулору за 1946 г., занялся такой игрой в один из знойных нью-йоркских летних дней у себя в конторе, увлекся этим и потом сообщил мне: «Я открыл ваши материалы в 9 часов утра, принялся за расчеты и чертежи. Короче говоря, только в 6 часов вечера я заметил, сколько времени прошло совершенно незаметно...»