Хронология
Каждое открытие обязано своим возникновением разуму, глазу, руке человека, а также благоприятным условиям окружающей среды, которые способствуют успеху исследования и доведению его до конца. Предложение новой системы мер в дополнение к метрической и футо-дюймовой представляется затеей в достаточной степени экстравагантной. С ним легче бы согласились, если бы оно было выдвинуто в итоге работы какого-либо съезда или конгресса. Однако эта мысль пришла в голову обыкновенному человеку, даже не профессионалу-изобретателю. Этот человек сорок пять лет работает как архитектор и живописец, т. е. в тех областях искусства, где все связано с мерой, где все измеряется.
С 1900 по 1907 г. он изучает природу под руководством замечательного педагога; наблюдает чудеса природы вдали от города, в горах Юра. При разнообразии природных явлений он обнаруживает в них определенные закономерности; в возрасте пятнадцати — двадцати лет проникается изяществом, мощью и гармоничностью природы.
В девятнадцать лет он отправляется в Италию, чтобы познакомиться с неповторимыми, причудливыми и тонкими произведениями искусства. Затем уже в Париже изучает строгую и вместе с тем смелую систему искусства средневековья и вытекающие из градостроительных основ закономерности искусства галантного времени Людовика XIV.
Двадцати трех лет автор нарисовал фасад дома, который собирался построить. Перед ним встал мучительный, повергший его в смятение, вопрос: «Какова же та закономерность, которая все определяет, которая связывает все воедино? Я,— говорит он, — стою перед проблемой чисто геометрической, я целиком во власти зрительных восприятий; на моих глазах складывается новое и самостоятельное явление. Льва узнают по когтям! А я не знаю, где сам лев и где его когти!»
Его охватили тревога и полная растерянность; он осознал свою беспомощность.
Однажды, сидя при керосиновой лампе в своей парижской комнатке, он рассматривал разложенные на столе художественные почтовые открытки. Его внимание привлекло изображение микеланджеловского Капитолия в Риме. Взяв другую открытку и перевернув ее лицевой стороной вниз, он интуитивно стал водить одним из ее углов (а угол-то прямой) по фасаду Капитолия. Внезапно перед ним открылась вероятная истина: быть может, вся композиция подчинена прямому углу и вписанные прямые углы определяют построение? Для него это было откровением, вызвавшим уверенность. Такой же проверке он подверг картину Сезанна. Но все же он еще не решается вынести окончательное суждение; он говорит самому себе, что композиция художественного произведения: должна подчиняться каким-то определенным правилам; эти правила могут быть строгими или сознательно более гибкими; они могут быть и шаблонными, применяемыми по привычке. Но они могут создаваться творческим инстинктом художника чисто интуитивно, как, по-видимому, рождена гармония в творениях Сезанна; человеком иного склада был Микеланджело: он предпочитал решения продуманные, научно обоснованные. В правильности предположений его убедила «История архитектуры» Огюста Шуази, многие страницы которой посвящены графическим методам построения. Он убедился в том, что такие графические методы действительно существуют.
В 1918 году автор стал серьезно заниматься живописью. Две первые картины написаны им, как бог на душу положил. Третья, написанная в 1919 году. была уже попыткой заполнить холст по определенной системе. Результат почти удачный. Четвертое полотно — откорректированное повторение третьего — было: написано с твердым намерением подчинить его построение строгим правилам. Был достигнут несомненный успех. В 1920 году создана серия полотен, выставленных в 1921 году в галерее Дрюе. Они уже строго подчинялись геометрической системе построения — в них использовались два чисто математических принципа: правило вписанного прямого угла и золотое сечение.
То были годы разработки этих математических начал и их плодотворного применения. В эти же годы автор в содружестве с рядом других лиц основал журнал «Эспри нуво». Он написал ряд теоретических статей, поскольку к концу первой мировой войны оказалось необходимым еще раз вернуться к разъяснению основных художественных принципов. Эту задачу и ставил себе журнал «Эспри нуво».
Вплоть до 1922 года, на шесть лет, автор забросил архитектуру и вновь занялся строительством лишь после опубликования в «Эспри нуво» ряда статей с изложением твердых теоретических положений, без которых не считал для себя возможным возврат к архитектурному творчеству. В его новых постройках проявились новые взгляды на задачи архитектуры: она должна выражать дух времени. В проектах были использованы методы графического построения (правда, в решениях только фасадов). Его исследования были комплексными и разносторонними: они охватывали основы градостроительства (проект «Современного города на 3 млн. жителей», 1922 г.), решение жилой ячейки, построение городской транспортной сети.
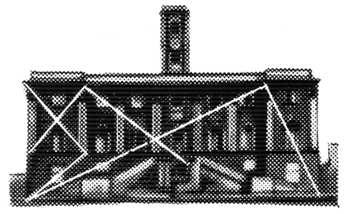
Во время своих путешествий он заметил, что во всех гармоничных произведениях как народных зодчих, так и квалифицированных архитекторов, высота жилых помещений в чистоте неизменно принимается 2,1—2,2 м (7—8 футов): он наблюдал это в жилых домах на Балканах и в Турции, в Греции, Тироле, Швейцарии и Баварии; такая высота помещений оказалась и в старых деревянных домах французской готики, в небольших квартирах Сен-Жерменского предместья, в Малом Трианоне, а также в традиционных парижских лавчонках времен Людовика XV и Реставрации, с их мансардами высотой также в 2,2 м. Это соответствует высоте человека с поднятой рукой и, следовательно, соразмерно масштабу человека. Автор не смог удержаться от того, чтобы использовать этот заманчивый размер в своих постройках даже в нарушение действующих правил. Один из членов муниципалитета крупного района Парижа заявил ему: «Мы разрешаем вам поступать вопреки нормам, поскольку знаем, что вы заботитесь о благе человека».
Журнал «Эспри Нуво» имел подраздел «Международный обзор современной деятельности». В статье оценивалась и обсуждалась взаимосвязь явлений и событий; вывод был таков: в наше время повсюду и во всем царит беспорядок. В делах, посвященных вопросам поощрения современного искусства, все приходится подчинять экономическим факторам. Большой шум был поднят вокруг статьи под заголовком «Строить серийно».
Речь шла о домах, названных мною «машина для жилья». Массовость, машинное производство, эффективность, себестоимость, темпы — все это были неизвестные доселе положения, настоятельно призывающие к установлению новой и строго обязательной системы мер (1921 г.).
«Эспри Нуво» взял на себя роль толкователя кубизма. — Это не техническое изобретение, которое могло подорвать социальные устои и экономику; то было раскрепощением, расцветом мысли; то было началом движения в будущее... пробил час разительных перемен в изобразительном искусстве. Эти перемены захватили и архитектуру.
Автор был самоучкой. Он постоянно избегал официального образования и поэтому никогда не признавал канонов, регламентированных и предписанных различными академиями. Свободный от духа академизма, он обладал широким кругозором, был весьма чутким к новым веяниям. Как кубист, он склонялся к пластике. Он мыслит «визуально». Происходя из семьи музыкантов, он даже не умеет читать ноты, но в душе он как никак музыкант и прекрасно понимает, как создается музыка; он может говорить о музыке и имеет свои суждения. Музыка, как и архитектура, существует во времени и пространстве. И музыка, и архитектура подвластны мере.
Много лет спустя, после опубликования в «Эспри Нуво» его статьи «Чертеж-регулятор» (Графические методы построения, 1921 г.), появилась книга Матилы Гика о пропорциях в природе и в искусстве, о золотом сечении. Он еще не был подготовлен к тому, чтобы следовать за приведенными в книге математическими доказательствами (алгебраические формулы и т. д.), но он прекрасно разобрался в смысле рисунков, которые, по существу, и представляли собой основное содержание книги Гика.
Профессор Цюрихского университета Андреас Шпейзер, занимающийся серьезными исследованиями в области групп и чисел, познакомил как-то автора со своей работой, посвященной египетским орнаментам, а также музыке Баха и Бетховена; все выводы и доказательства в работе были обоснованы математически. Автор сказал тогда профессору: «Я вполне согласен с тем, что природа подчиняется законам математики, и с тем, что шедевры искусства созвучны природе.
Следовательно, произведения искусства также служат своего рода отображением математики, и ученые получают право распространять и на искусство непреложные математические положения и формулы.
Художник обладает исключительной, беспредельно развитой восприимчивостью; он чувствует и познает природу, преломляя и отражая ее в своих произведениях. Он одновременно — и жертва, и выразитель своей судьбы. Вы, например, математически доказываете совершенство египетской орнаментальной композиции в труде, посвященном математике. Если бы мне как художнику предложили вписать подобный орнамент в такую же полосу, я неизбежно пришел бы к такому же его построению, поскольку оно предопределено сущностью самого орнамента. Оно входит в ограниченное число возможных решений, в основе которых лежит геометрическое построение, обусловленное самой природой человека, и являющееся, как и сам человек, одним из проявлений законов природы».
Большое внимание, уделенное автором этим вопросам, принесло ему в 1933 году совершенно неожиданное признание: в связи с празднованием шестисотлетнего юбилея Цюрихского университета, ему была присуждена степень доктора математических наук в знак признания его заслуг в области исследования построения форм и пространства. В 1945 году, после ряда лет вынужденного молчания, в своей работе «Невыразимое пространство» автор следующими словами попытался выразить сущность того, что его волнует: «Овладеть пространством — таково первое побуждение всего живого».
Цветок, растение, дерево, гора тянутся вверх, живя в своей среде. Их облик привлекает к себе внимание своим подлинным величием и выразительностью. Мы останавливаемся, ощутив взаимосвязь явлений в природе, с волнением наблюдаем гармонию, которой охвачено столь большое пространство; лишь позднее мы начинаем оценивать, измерять все то, что находится в поле зрения.
Архитектура, скульптура, живопись целиком связаны с пространством, с необходимостью организовать пространство, каждая своими средствами. Самое существенное здесь то, что ключом к эстетической эмоции служит восприятие пространства.
Воздействие произведения искусства (будь то здание, скульптура или живописное полотно) бывает различным: оно может захватывать, как морские волны, вызывать возгласы восторга и восхищения (Парфенон в Акрополе в Афинах), озарять все вокруг лучами света или отблесками взрыва. Все окружение потрясено, взволновано, подчинено или обласкано. Окружающая среда поддается воздействию художественного произведения; оно оказывает влияние на стены помещения, в котором оно находится, на облик площади с выходящими на нее различными по значимости фасадами зданий; произведение искусства, порожденное волей человека, накладывает свой отпечаток на окружение, определяя проникновенность или порывистость, четкость или расплывчатость, суровость или нежность его характера.
Возникает гармоническое отношение, совершенно такое же, как в математике, — выражение подлинного художественного созвучия, да будет мне позволено применить этот музыкальный термин.
«Ни на что не претендуя, я ратую за возвеличение роли пространства, к которому со столь явным творческим успехом обратились художники моего поколения, создавшие около 1910 года кубизм. Они с большей или меньшей интуитивной прозорливостью говорили о четвертом измерении. Посвятив свою жизнь искусству, и в особенности поискам гармонии, я считаю себя в праве, на опыте работы в трех областях искусства (архитектуре, скульптуре и живописи), высказать свои соображения по данному вопросу. Представление о четвертом измерении является поворотным пунктом и вызвано исключительным развитием пластических средств в искусстве. Открывается беспредельная глубина, устраняются все преграды, упраздняются всяческие условности и возникает несказанное чудо пространства.
Я не верю в чудеса, но часто ощущаю чудо невыразимого пространства, венчающее художественные эмоции».
В предвоенные годы, в период между 1925 и 1933 гг., во Франции развернулось интенсивное строительство, и автор ощутил стремление и потребность создавать архитектурные произведения, соразмерные человеческому масштабу. На стене своей мастерской он начертил метрический масштаб высотой 4 м; с ним он мог сопоставить свой рост и соизмерять нарисованную в натуральную величину человеческую фигуру в разных положениях. Этот эксперимент показал, что метр — всего лишь условная величина, успешно используемая в десятичной системе; однако это величина абстрактная, непригодная для назначения в архитектуре размеров. Метр может стать даже средством опасным; по невниманию или лени легко соблазниться его приспособляемостью к абстрактным числам и закрепить навеки столь удобные для пользования размеры, как метр, полметра, четверть метра, дециметр и т. д. Это и произошло постепенно в ходе последнего столетия — века упадка архитектуры.
Автору пришлось столкнуться с системой стандартизации АФНОР (Французское общество стандартизации. AFNOR — Associaation Francaise de Normalisation). Промышленники, инженеры и архитекторы объединились для решения вопросов стандартизации, в частности в области строительства. Автора не привлекли к участию в работе АФНОР, хотя двадцатью годами ранее (и его за это обвиняли) он писал: «Для решения проблемы совершенствования необходимо стремиться к стандартизации». Парфенон — результат совершенствования стандарта, сложившегося типа храма. Архитектура пользуется стандартом. Стандарты создаются на основе логики, анализа, тщательных исследований; они являются ответом на хорошо поставленное задание. Окончательному принятию стандарта должна предшествовать экспериментальная проверка».
Глаза, которые не видят. «Эспри Нуво», 1920 г. и «К архитектуре», 1923 г.
«Крупная промышленность должна заняться строительством и организовать поточное производство элементов зданий. Нужно полностью осознать необходимость поточного производства: проникнуться нужностью массового серийного строительства домов, понять неизбежность проживания в типовых домах серийного производства, заняться проектированием типовых домов для массового серийного строительства».
(Серийный дом. «Эспри Нуво», 1921)
Для этого необходимо создать новые нормы проектирования и строительства. Возникает бездна проклятых вопросов!
Париж был оккупирован, а Франция оказалась расчлененной демаркационной линией на две части. Моя мастерская была закрыта 11 июня 1940 г. Целых четыре года мне не поручали никаких проектных и строительных работ. Это побудило меня усиленно заняться в обществе АСКОРАЛ (Assamblee des constructeurs pour une renovation architecturale (Общество обновления архитектуры), основанном в конце 1942 г. Заседания одиннадцати секций и подсекций этой организации проводились дважды в месяц, в укромных местах, укрытых от любопытных глаз. Объема проработанного материала хватило бы на десяток книг.
Секция этого общества «Теория жилища» состояла из трех подсекций: оборудование жилища; стандартизация в строительстве; индустриализация строительства*.
* Вышли в свет или были подготовлены к печати следующие труды: «На перепутье», 1941; «Афинская Хартия», 1942; «Дом для человека», 1942; «Беседы со студентами», 1942; «Мысли о градостроительстве», 1943—1946; «Три формы расселения», 1943—1946; «О градостроительстве», 1945. Многие из этих книг были переведены на английский, испанский, итальянский, датский и другие языки.
Один из моих молодых коллег, Ханнинг, был вынужден в 1943 г. скрываться в Савойе, по ту сторону демаркационной линии. Он попросил дать ему задание, которым мог бы заняться в свободное время. Этот славный молодой человек работал в моей мастерской с 1938 г.; он хорошо понимал смысл поисков пропорциональности, которыми мы уже давно занимались. «АФНОР предлагает стандартизировать строительные элементы зданий, — сказал я ему, — эта организация намечает слишком упрощенный, чисто арифметический метод, нечто среднее из того, что уже применяют архитекторы, инженеры и строители. Он кажется мне и произвольным, и к тому же убогим. Посмотрите, например, на деревья с их стволами, ветвями, листвой, прожилками на листьях; они свидетельствуют о том, что их развитие и формы подчинены закономерностям, отличающимся значительным и тонким разнообразием. Они, безусловно, связаны какими-то математическими соотношениями.
Я мечтаю установить на всех строительных площадках, которые неизбежно возникнут в нашей стране, специальную «пропорциональную сетку», начерченную на стенке или сваренную из полосовой стали, которая стала бы на строительстве законом, эталоном для определения бесконечного числа возможных сочетаний и пропорциональных отношений. Каменщик, плотник или столяр могли бы всегда воспользоваться этой сеткой для уточнения размеров своих изделий; тогда все эти разнообразные и отличные друг от друга изделия обретут гармоничную соразмерность. Такова моя мечта.
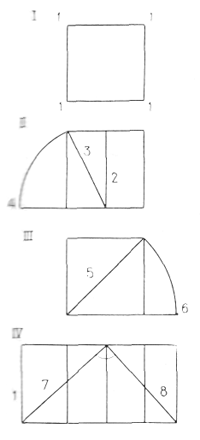
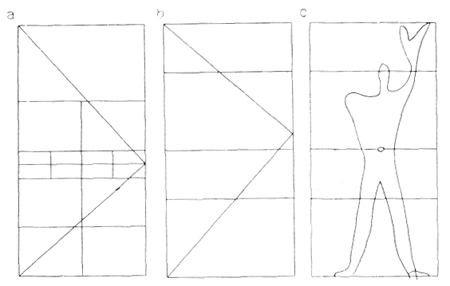
Представьте себе человека с поднятой рукой общей высотой 2,2 м. Впишите такую фигуру в два, поставленных один на другой, квадрата со сторонами 1,1 м каждый; впишите в эти два квадрата третий, который поможет вам найти искомое решение. Правило вписанного прямого угла определит положение третьего квадрата. Я убежден, что такая основанная на размерах человека сетка, установленная на строительных площадках, поможет определить систему размеров, согласующихся с ростом человека с поднятой рукой и математическими соотношениями». Таковы были мои инструкции, данные Ханнингу. 25 августа от него поступило первое предложение (рис. 2):
I — квадрат;
II — золотое сечение;
III—диагональ квадрата, перенесенная на его основание;
IV — построение А; вершина прямого угла совмещена с верхней точкой вертикали, делящей исходный квадрат на две равные части.
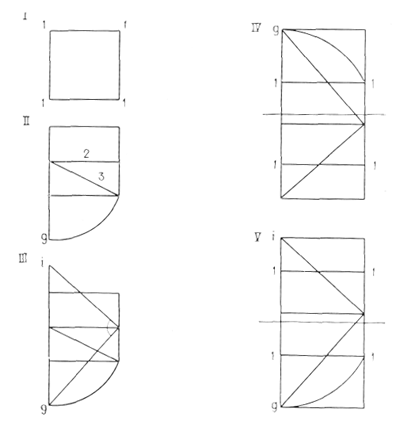
Над этой проблемой работал также АСКОРАЛ (секция IIIб и, в частности, Элиза Майяр *). 26 декабря 1943 г. было предложено следующее откорректированное построение (рис. 3):
I — квадрат;
II — построение отрезка в отношении золотого сечения к стороне квадрата;
III — совмещение вершины прямого угла с осью основного квадрата определяет положение точки i;
IV — линию g — i делим на две равные части;
V — получаем два смежных квадрата, каждый из которых равновелик исходному квадрату **.
*Элиза Майяр — сотрудница парижского музея Клюни и автор замечательного труда о графических методах построения «О золотом сечении».
**В конце книги приведено доказательство равновеликости трех квадратов, использованных в приведенном построении.
 |
 |
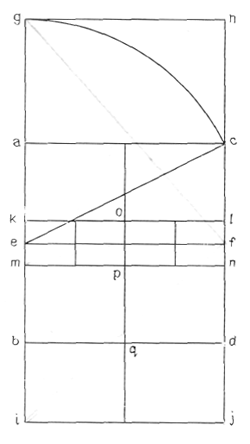
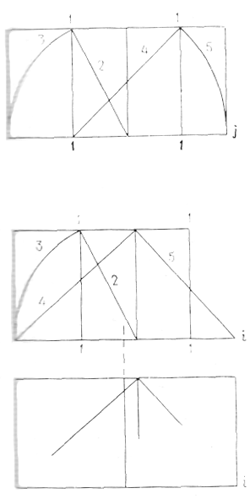
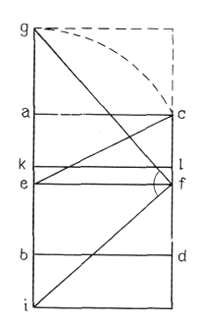
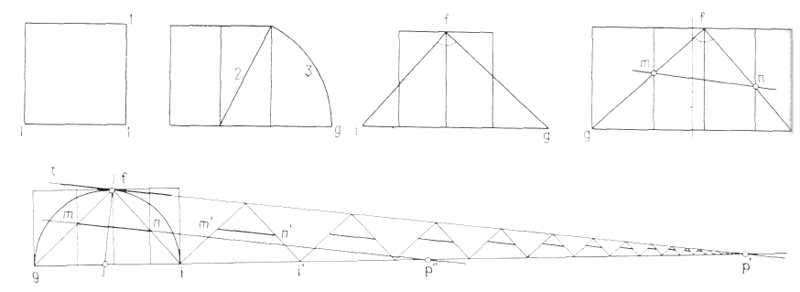
Прямая g — i делится на отрезки, имеющие весьма существенное значение, отношения которых обладают большим разнообразием. Но нам представляется, что они еще не образуют четкой системы. На основании рис. 4 можно установить следующее: abcd — исходный квадрат;
ef — его медиана;
с точкой f совмещена вершина прямого угла, одна из сторон которого проходит через точку g;
в точке i вторая сторона прямого угла пересекает продолжение прямой gb;
bdij — два смежных прямоугольника, стороны которых bi и dj находятся в отношении Ø к диагоналям iq и qi; kl — горизонтальная медиана прямоугольника ghji; mn расположена симметрично по отношению к kl;
Прямоугольник klnm, разделенный пополам вертикальной медианой op, образует прямоугольники kopt и olnp; длина общей диагонали к длине диагонали половины прямоугольника находится в отношении Ø;
Прямая gi делится в точке m в отношении Ø; в точке m основание исходного квадрата abcd делится в отношении Ø; в точке k в том же отношении делится сторона того же квадрата abcd; kl — медиана прямоугольника ghji.
 |
 |
 |
 |
На прямой gi пять отрезков, входящих в возрастающий пропорциональный ряд:
km; ga = am = kb;
ka = mb = bi; gk = ki, gb.
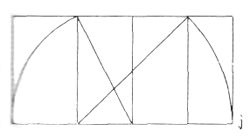
Поскольку gk = ki — смежные квадраты, gklh и klji равновелики и равновелики исходному квадрату abcd. Итак, решена поставленная задача—разместить в двух смежных квадратах, соответствующих человеку с поднятой рукой, третий квадрат «в месте прямого угла». Чертеж (a) может быть перевернут (b), и в этом случае он будет иметь вид (c).
Перед нами две, как будто одинаковые, схемы построения, полученные, однако, в результате следования различным ходам мысли; построение Ханнинга основано на двух диагоналях исходного квадрата; в основу схемы Майяр положено отношение Ø , возникшее путем переноса дигонали квадрата и определения положения точки i путем вписания прямого угла. Точка i устанавливает наличие двух смежных квадратов, равновеликих исходному.
По схеме Ханнинга определяется положение точки j, не совпадающее в точности с положением точки i. Таким образом, создалась пропорциональная сетка, в которой недостаточно выясненной осталась роль точек i и j. Она предназначена для использования на строительных площадках; с ее помощью можно будет устанавливать множество размеров, находящихся в гармоничных соотношениях, которыми можно пользоваться при назначении размеров помещений, дверных проемов, шкафов, окон и т. д. Создается возможность придать бесконечное разнообразие соотношений в размерах изделий серийного производства и получить легко сочетаемые и сопрягаемые сборные элементы заводского изготовления.
В мастерской на ул. Севр вновь приступили к разработке типовых жилых ячеек, которые впервые были показаны еще в 1922 г. (тип «индивидуальный жилой дом»), а затем повторно в 1925 г. на Международной выставке декоративного искусства в Париже (в павильоне «Эспри Нуво»); они, наконец, были использованы в 1937 г. в проекте реконструкции «трущобного квартала № 6».
Пропорциональная сетка дала возможность с исключительной уверенностью назначать проектные размеры. Была, таким образом, создана система размеров для элементов плоскости, приводящая во взаимосвязь математические величины с размерами человеческой фигуры. Мы широко использовали эту систему, но все-таки сохранилось чувство неудовлетворенности; системе не хватало четкости.
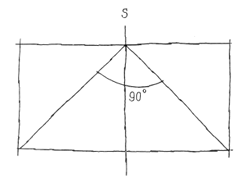
По правде говоря, мы даже не смогли прийти к единому мнению. 10 марта 1944 г. в своем письме из Савойи Ханнинг сообщил мне, что графическое построение «Майяр — Ле Корбюзье» математически невозможно: местоположение вершины вписанного прямого угла может находиться лишь в точке S, на общей для смежных квадратов линии. Существует лишь один вписанный прямой угол, образованный диагоналями двух смежных квадратов»... Это утверждение противоречит его собственному чертежу от 25 августа 1943 г., на котором показаны образующие прямой угол наклонные 7 и 8 (см. рис. 6). Эти наклонные прямые вновь появятся на чертеже в августе 1948 г. и получат, как мне кажется, полное обоснование.
Читателю следует себе представить обстановку, в которой проводилась эта работа: Париж оккупирован немцами; люди были разобщены, и собираться было крайне трудно. В этих условиях организовать дискуссии на архитектурные темы среди специалистов было почти невозможно. Закон обязал меня выдвинуть свою кандидатуру в члены Корпорации архитекторов, созданной в конце 1940 г. Рассмотрение моего заявления затянулось на 14 месяцев, вплоть до лета 1944 г., когда со стороны Версаля уж доносились выстрелы английской артиллерии. Работа различных комиссий АСКОРАЛ проходила при свечах в нетопленой, пыльной, заброшенной мастерской на ул. Севр, 35; телефона не было. Секция стандартизации продолжала свою работу. Иногда до нас доходили сведения о работе официальной организации АФНОР. Руководитель секции IIIб АСКОРАЛ, состоявший одновременно членом АФНОР, держал меня в курсе дел и писал мне 16 октября 1943 г.: «Между точками зрения АСКОРАЛ и АФНОР имеется существенное расхождение — одни стремятся к лучшему из всех возможных решений; вторые — к среднему из того, что уже имеется».
Наступил 1944 год — год освобождения. Осенью я был включен в состав Теоретической комиссии Национального фронта архитекторов и добился, чтобы Афинская хартия CIAM была положена в основу дискуссии по вопросам восстановления, строительства, заводского изготовления элементов зданий и согласования их размеров. Настоятельная нужда в пропорциональной сетке становится все более очевидной.
7 февраля 1945 г. г-жа Майяр и я посетили г-на Монтеля, декана факультета естественных наук Сорбонны, и показали ему чертеж нашей сетки. Он сказал: «Раз вы вписали прямой угол в два смежных квадрата, вы ввели математическую величину √5. Это приведет к широкому использованию отношений золотого сечения».
 |
 |
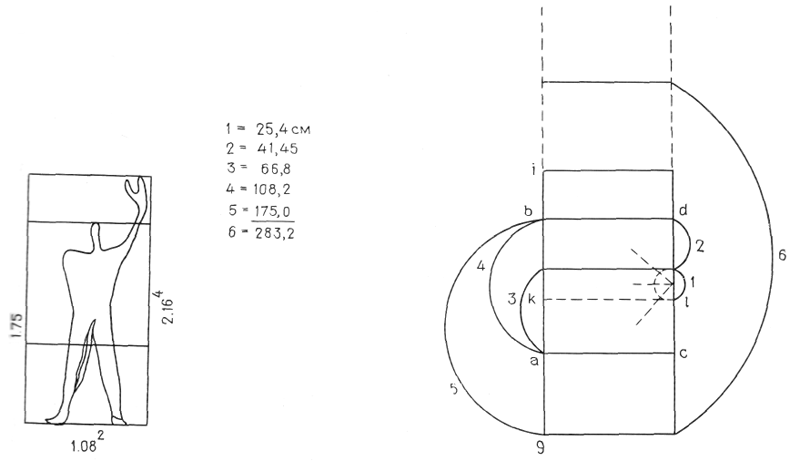
С 30 марта 1945 г. я вновь серьезно занялся пропорциональной сеткой. В работе приняли участие Воженский, Ханнинг, Ойам и Лоос. Управление культурных связей Министерства иностранных дел обратилось ко мне с просьбой организовать и возглавить группу архитекторов для поездки по США. Мне очень хотелось взять с собой пропорциональную сетку, которая могла бы стать средством для назначения размеров сборных строительных деталей заводского изготовления.
Мы разработали несколько таблиц, иллюстрировавших, как нам казалось, все разнообразие возможных сочетаний таких изделий. Мы придали открытой нами геометрической форме человеческий облик, приняв за основу рост человека в 175 см. Пользуясь сеткой, определили ряд пропорциональных размеров 175—216,4—108,2 см, отвечающих порядковым числам 1, 2, 3, 4 и т. д. возрастающего ряда чисел с отношением Ø.
Легко заметить, что эти числа отвечают одному из рядов, называемому рядом Фибоначчи, в котором сумма двух смежных чисел равна последующему числу. Мы тогда же запатентовали наше открытие. Некоторые подробности того, как это происходило, представляют несомненный интерес.
 |
Мне было трудно дать сжатое, простое и доходчивое разъяснение принципа построения пропорциональной сетки. Приходилось беседовать с совершенно незнакомым мне директором Патентного агентства, инженером по образованию, не подготовленным к восприятию смысла подобных исследований. Как заставить его понять, что мы нашли направление, которое уже дало первые результаты? Как объяснить ему, что мы стоим перед дверью, за которой что-то свершается, но что у нас еще нет ключа, которым можно открыть эту дверь и познать смысл происходящего?
— Мсье, — обратился я к нему, — разрешите в первую очередь признаться, что по тысяче причин и на основании жизненного опыта я не поклонник патентов на изобретения. Я тем не менее хочу побеседовать с вами о пропорциональной сетке и тому подобном, выраженном в числах, цифрах и чертежах-диаграммах; но я не нашел еще точного определения для всего этого или, если хотите, надлежащего объяснения. В том, что я вам сейчас доложу, вы ничего не сможете понять. Если вы сочтете нужным, я готов повторить все это еще два или три раза. Если и после третьего раза вы не увидите во всем этом ничего интересного, вы выставите меня за дверь.
Так все и произошло; я объяснил один, потом второй раз.
— Сожалею, но ничего не понимаю. Объясните третий раз.
Потом он сказал: «Минуточку, я начинаю понимать и мне это представляется крайне интересным и важным и т. д.». Прощаясь, он сказал: «Для меня, инженера по патентам, час, проведенный с вами, будет самым знаменательным за все годы работы». Мой собеседник уяснил себе неоспоримые достоинства и значение данного изобретения.
Проходили недели. Прошел год. За это время я передал право на реализацию нашего изобретения весьма толковому и высокоэрудированному человеку; я предполагал использовать изобретение в послевоенном массовом сборном жилищном строительстве. Я все яснее представлял себе положение вещей и без излишнего честолюбия пришел к убеждению, что наша пропорциональная сетка, положенная в основу массового заводского изготовления строительных элементов, может привести к примирению и согласованию метрической системы мер с системой футов и дюймов.
Деловые люди говорили мне: «Вы имеете право на определенные отчисления от стоимости всего, что будет построено с использованием вашей системы мер».
Открывались огромные, почти блестящие перспективы! Мой доверенный добился использования изобретения во многих странах Европы и Америки. Он подготовил открытие представительств во многих странах мира.
Однажды он мне сказал: «Ваши числовые величины чрезмерно жестки. Они не отвечают точным размерам, выраженным как в метрической системе, так и в системе фута-дюйма; они не увязываются также с системой АФНОР. Если бы вы придали вашим числовым величинам больше гибкости и разрешили допуск в пределах 5 % в ту и другую сторону, все были бы довольны и все пошло бы без сучка и задоринки».
Под знаком этого ужасного предложения прошел весь 1945 год!
А впереди еще путешествие в США, через Атлантический океан, на грузовом судне «Верной С. Худ».
Как-то в 1946 г. я попросил своего друга Андре Жауля, сотрудника электрохимического предприятия в Южине, пойти со мной к инженеру по патентам. Я заявил этому чудесному человеку: «Хочу вас заверить при свидетеле, что не собираюсь наживать состояния на своем изобретении. Денежный вопрос не должен иметь значения при решении моего дела. Поймите меня: я хочу спокойно заняться разработкой вопросов, связанных с пропорциональной сеткой, попытаться ее внедрить в практику и, в самых обычных условиях, убедиться лично в ее достоинствах и недостатках, заняться ее доработкой и совершенствованием. Меня не интересует коммерческая сторона дела, и я не нуждаюсь в рекламе. Суть моего изобретения такова, что если оно действительно стоящее, то мои друзья-архитекторы во всем мире будут им пользоваться, а лучшие архитектурные журналы всех стран отведут на своих страницах место для его оценки и ознакомления с ним своих читателей. Я великолепно сознаю свою ответственность и не считаю возможным подчинить это дело проклятому, дикому и бессовестному духу стяжательства. В этом вопросе я крайне щепетилен. Я рассчитываю на то, что архитекторы и строители будут применять эту полезную систему мер. Пусть этот вопрос будет обсуждаться на широких совещаниях, если он этого заслуживает, пусть его передадут на рассмотрение в экономическую и социальную секцию ООН. Кто знает, быть может, наступит время, когда трудности и препятствия, соперничество и возражения, возникшие на почве антагонизма двух действующих систем мер — фута-дюйма и метра — придут к концу, и наше предложение сможет объединить то, что было враждебным друг другу, станет средством их согласования и примирения.
 |
Вам, конечно, понятно, что я не смогу продолжать свою деятельность, которая может стать своего рода апостольской, если буду знать, что каждый мой призыв, каждое мое выступление, каждое новое достижение будет сопровождаться отчислениями в мою пользу. Я не сборщик податей!»
Это свидание разрешило проблему; могу заверить читателей, что в соответствии с этим решением, после 1945 г., года блестящих финансовых перспектив, она уже для меня не существовала; я почувствовал большое облегчение, совесть стала чиста и спокойна; в конце концов не это ли дает нам высшее удовлетворение?
У себя в мастерской я поручил Андре Воженскому и Солтану подготовить материалы к предстоящей поездке в США. Солтан был новичком в этом деле и не знал всей предыстории вопроса. Он не имел представления о двух смежных квадратах и вписанном в них третьем квадрате и т. д. Вскоре же, ознакомившись с материалами, он сказал: «Мне представляется, что ваше изобретение относится только к величинам линейным и не может быть распространено на плоскость. Изобретенная вами пропорциональная сетка — лишь фрагмент линейного ряда чисел, находящихся в отношении золотого сечения и стремящегося к нулю, с одной стороны, и к бесконечности — с другой». «Прекрасно, — ответил я ему, — отныне будем именовать его «линейкой пропорций». Теперь все стало еще яснее. Солтан нанес на ленту деления от нуля до 2,164 м, что соответствует росту человека с поднятой рукой 1,75 м. 9 декабря 1945 г. я сделал первую попытку изобразить открытое нами правило графически. Вскоре мы погрузились на судно типа «Либерти», принадлежащее фирме «Vernon S. Hovd». Оно вышло из Гавра в середине декабря 1945 г. и пришло в Нью-Йорк после 19 дней плавания. Первые шесть дней был ужасающий шторм; остальное время сохранялось очень сильное волнение.
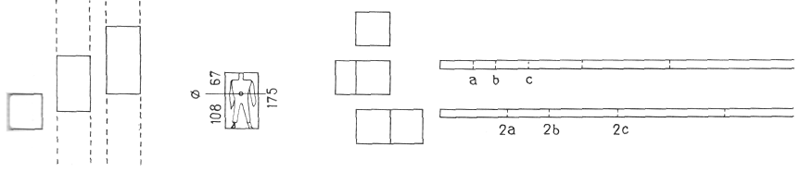 |
Я сказал ехавшему со мною Клодиусу Пети*: «Я не сойду с этого проклятого судна до тех пор, пока не найду подтверждение своему правилу золотого сечения». Один любезный пассажир договорился с командованием судна о предоставлении в наше распоряжение одной из кают ежедневно с 8 до 12 и с 20 до 24 ч. Там, под рев шторма, я пытался найти связь между последовательно возникавшими мыслями. С собой у меня была изготовленная Солтаном лента, которую я хранил в небольшой алюминиевой коробочке; с тех пор я постоянно держу ее в кармане. Зачастую в самых неожиданных местах я вынимаю из коробочки магическую ленту с тем, чтобы проверить те или иные размеры.
* Клодиус Пети (Claudius Petit) — бывший министр реконструкции Франции, во многом содействовавший Ле Корбюзье в осуществлении ряда его проектов. (Прим. пер.).
Однажды, например, когда некоторые из нас расположились на капитанском мостике, я вытащил из коробочки ленту и, сидя на корточках, сделал проверочные замеры. Все вокруг представлялось удачно и целесообразно соразмерным.
Весной 1948 года я сделал еще одну проверку. Участвуя в заседании Экономического совета отдела реконструкции, планировки и общественных работ, на котором обсуждался новый закон о квартирной плате, я выдвинул предложение о высоте жилых помещений, равной высоте фигуры человека с поднятой рукой, и об удвоенной такой высоте. Заседание проходило в Пале-Рояле в Париже, на этаже, где размещались «малые апартаменты» (конца XVIII и начала XIX века). Их высота вполне была бы достаточна для новых небольших квартир, поскольку она вполне устраивала нас, заседавших. Я вытащил свою ленту и измерил высоту от пола до потолка. Председатель совета г-н Како убедился в том, что этот размер полностью отвечает моему предложению.
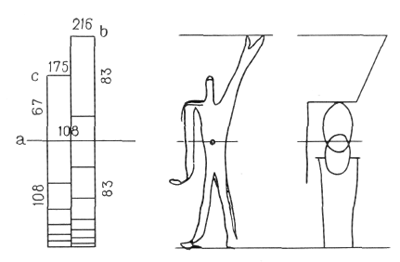
Вернемся, однако, к нашему грузовому судну. В условиях жестокой качки я начертил шкалу чисел. Эти числа соответствовали отношению основных частей человеческой фигуры в пространстве, и потому они антропоцентричны. Отвечают ли эти числа каким-либо особым и наиболее характерным математическим величинам? На этот вопрос дают ответ рисунки 13 и 14.
 |
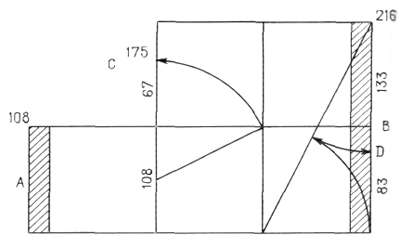 |
Единица измерения..... А = 108
Удвоенная величина..... В = 216
Отношение..... Ø А = С = 175 (108 Ø 67)
»..... Ø В = D = 83 (133 Ø 83)
Теперь можно смело утверждать, что это правило фиксирует положение характерных точек человеческой фигуры в пространстве и что оно представляет собой простейшее и наиболее важное математическое; преобразование единицы измерения, а именно: единица, ее удвоенная величина и их увеличение или уменьшение на величины, находящиеся с ними в отношении золотого сечения.
Мы обрели значительно большую уверенность и заметно продвинулись по сравнению с тем временем, когда в месте наложения прямого угла пришли к вписыванию третьего квадрата в два равновеликих ему смежных квадрата.
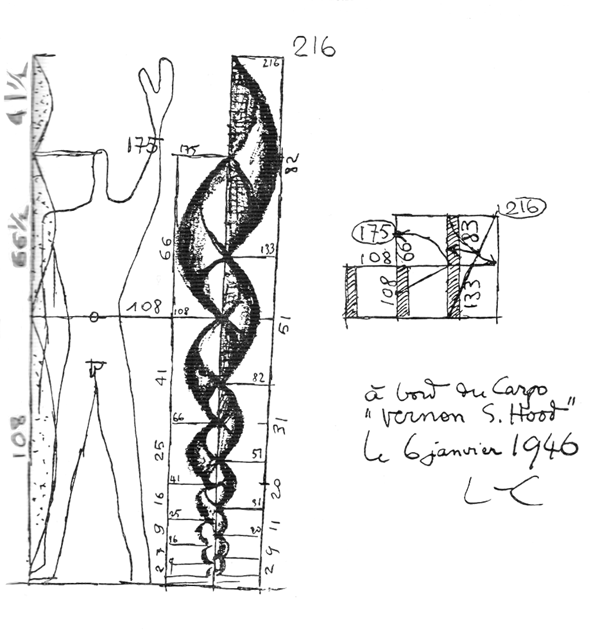
Разместив обе схемы на одном чертеже, получили весьма интересный рисунок, выполненный мною на борту «Верной С. Худ» 6 января 1946 г. Я дал название Красного ряда — ряду Фибоначчи, построенному на соотношении Ø при исходной величине 108 и Синего ряда — такому же ряду при удвоенной исходной величине 216. Затем я нарисовал фигуру человека ростом 1,75 м; четыре ее характерные точки зафиксированы на высоте: 0,108, 175 и 216. Рядом с фигурой я начертил красный (слева) и синий (справа) ряды величин, находящихся в отношении Ø, стремящихся к нулю книзу и к бесконечности кверху.
По возвращении во Францию я поручил Превералю, работнику моей мастерской, привести в порядок заметки, сделанные мною на борту «Вернон С. Худ».
 |
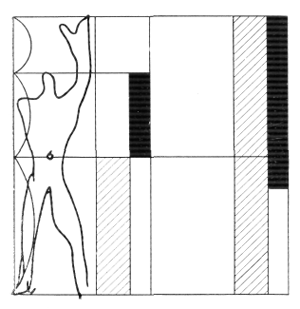
Надо было дать нашей шкале золотого сечения краткое и доходчивое название. Из многих вариантов мы остановились на МОДУЛОРЕ. Одновременно была выработана эмблема, как бы «фирменный знак», рисунок, поясняющий сущность изобретения.
Придумать эмблему было нетрудным делом, поскольку Модулор служит средством назначения размеров, связанных с размерами человеческой фигуры и математическими закономерностями. Человек с поднятой рукой определяет положение в пространстве характерных точек фигуры — стопы, солнечного сплетения, головы, конца пальца поднятой руки, образующих три интервала, которые подчинены одному из рядов золотого сечения, называемому рядом Фибоначчи. Они, кроме того, отвечают простейшему и наиболее надежному математическому методу назначения размерных величин: основная единица, ее удвоенная величина и два ее отрезка при делении в отношении золотого сечения.
 |
Практическое применение Модулора показало возможность получения бесконечного числа сочетаний. Превералю было также поручено подготовить несколько плакатов. Достигнутый великолепный результат был естественным выводом из свойств чисел, из строгих и чудесных математических закономерностей. Нас попросили округлить числа, с тем чтобы сблизить их с некоторыми общеупотребительными размерами. Нас упрекали в основном в следующем: числа, нанесенные на первой модульной ленте, изготовленной Солтаном, и приведенные к первоначальной числовой таблице, отвечали метрической системе, как, например, размер 1080 мм — до точки солнечного сплетения. К сожалению, было невозможно перевести эти метрические величины в систему фут-дюйм. Вместе с тем Модулор рассчитан на то, чтобы в один прекрасный день стать унифицированной системой для назначения размеров промышленных изделий во всех странах света. Необходимо было нанести величины, выраженные в футах и дюймах.
Я никогда не предполагал округлять отдельные числа обоих рядов, красного и синего. Однажды, когда мы погрузились в совместные поиски решения, один из нас, архитектор Пей, сказал: «Размерные величины Модулора в его сегодняшнем виде определяются ростом человека в 1,75 м. Этот средний рост типичен для французов. Не обращали ли вы внимание на то, что высота рослых мужчин, например полисменов в английских детективных романах, всегда принимается в шесть футов!» Мы попробовали исследовать этот эталон: шесть футов = 6х30,48 = 182,88 см. К нашему восторгу, деления шкалы нового Модулора, основанного на фигуре человека ростом шесть футов, легко определялись в целых футах и дюймах.
Уже было доказано (главным образом в эпоху Возрождения), что строение человеческой фигуры подчинено пропорциям золотого сечения. Когда англосаксы установили свои линейные меры, было определено соотношение между величиной фута и дюйма, причем это соотношение скрытно распространялось и на размеры соответствующих частей человеческой фигуры. Теперь мы направили усилия на округление числовых значений нового Модулора, основанного на росте человека в 6 футов (182,88 м).
Получилась следующая таблица:
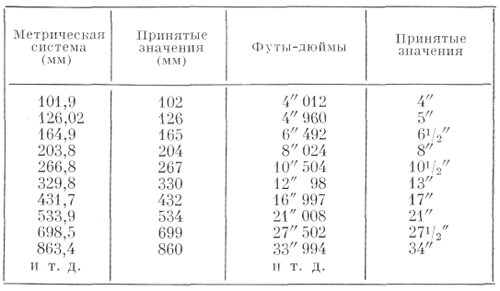
Результат привел нас в восторг. Солтан разграфил новую размерную ленту, на этот раз в ее уже окончательном виде; она заменила первую, в алюминиевой коробочке, которую я всегда носил в кармане.
Мы поняли, что Модулор может автоматически содействовать преодолению мучительных расхождений при пользовании метрической системой и системой фута-дюйма. В жизни эти расхождения столь значительны, что образуют непреодолимую преграду между специалистами, применяющими ту или другую систему мер*.
* Я помню, сколько трудностей пришлось мне перенести при проектировании в 1947 г. комплекса зданий ООН в Нью-Йорке. Тот, кто сам был не жертвой неприятностей и трудностей, связанных с несоизмеримостью этих систем мер, не способен оценить серьезность указанных вопросов.
Перевод расчетов из одной системы в другую — работа дорогостоящая и трудоемкая; она в еще большей степени разделяет сторонников разных систем, чем даже различие в языке.
С помощью Модулора переход с метрической системы на систему футов-дюймов происходит автоматически. Он не только согласует с футами и дюймами метр, представляющий собой не что иное, как условную длину металлического стержня, хранящегося на дне колодца павильона Бретей близ Парижа *, но и упрощает пользование системой фута-дюйма и перевод ее на десятичную систему, избавляя от сложных, утомительных, угнетающих действий сложения, вычитания, умножения и деления.
* Отметим, что сейчас абсолютным эталоном метра служит длина определенной цветовой волны.
«Мы должны отдать должное методу отсчета путем установления нулевой позиции. Без этого арифметика никогда не смогла бы освободиться от пут, установленных еще при греках. Его благотворное влияние сказывается не только на математических расчетах, но и во всех областях техники, на которых зиждется могущество современных великих держав» (Франсуа Ле Лионнэ. Красота математики, 1948). Первого мая 1946 года я вылетел в Нью-Йорк, чтобы защищать по поручению Французского правительства в Объединенных Нациях современную архитектуру в связи с проектированием и строительством здания ООН.
Большое удовлетворение мне доставили довольно длительные беседы с профессором Альбертом Эйнштейном о Модулоре. Я еще переживал время неуверенности и беспокойства и поэтому неудачно изъяснялся, порой плохо объяснял, путал причины и следствия. Эйнштейн вооружился карандашом и стал; делать расчеты. По глупости я помешал ему в этом и перевел разговор на другую тему; расчеты оказались прерванными.
Друг, который меня привел к Эйнштейну, был в отчаянии. В тот же вечер Эйнштейн прислал мне любезное письмо, в котором о Модулоре было сказано: «Это гамма пропорций, мешающая делать плохо и: помогающая делать хорошо». Некоторые считают, что это высказывание лишено научности. Я же считаю его исключительно прозорливым. То был дружеский жест великого ученого в наш адрес и в адрес всех тех.: кто является не ученым, а солдатом на поле брани. Ученый как бы говорит нам: «Из этого оружия вы попадете точно в цель; в деле назначения размеров, а следовательно пропорций, оно придаст вашей работе уверенность».
В бюро консультаций на Бродвее я разъяснил Модулор Мужо, основавшему в Париже Экономический; организационный комитет с филиалом в США, занимавшийся организацией промышленного производства. Я спросил его: «Как это случилось, что вы, француз, взялись за организацию американского промышленного производства?»
«Да потому, что здесь в этой области царит поразительная бесхозяйственность. Каждый день узнаешь что-то неожиданное». Несколько позже Мужо сказал мне: «Я провел целый день за расчетами с помощью вашего Модулора; знаете ли вы, что в интервале между минимальным размером, учитываемым в настоящее время и равным пятнадцати тысячным миллиметра, и длиной окружности земного шара Модулор предусматривает всего навсего 270 градаций? Это любопытно». Он добавил: «Модулор должен применяться не только в архитектуре, но с полным правом и в механике. Ведь машиной управляет человек, и она всецело зависит от движений рабочего; она, следовательно, должна соответствовать человеческому масштабу. В механике необходимо использовать такие измерения, которые помогли бы определить оптимальные габариты самой машины и необходимого рабочего пространства, которые продиктуют фактические размеры машины, а следовательно, и размеры ее составных частей: ведущего вала, станины, кожуха и т. п.». Этот вывод Мужо крайне важен.
В Нью-Йорке я посетил Музей Купера, который используют при прохождении курсов декоративного искусства и архитектуры. В отделе мебели я задержался в салоне Людовика XV, украшенном гротесками* чудесных пропорций. Я извлек из кармана свою размерную ленту и промерил высоту комнаты: она оказалась равной точно 2,16 м; размеры камина и других предметов обстановки салона также в точности отвечали моей шкале размеров. Сопровождавшей меня знакомой я заявил: «Это безусловно работа столяра-француза, поскольку я пользовался лентой № 1, в основу которой положен рост человека в 1,75 м. На таблице аннотации было указано: «Singerie** из замка Шантильи».
* Термин гротеск (grotesque) происходит от слова грот (grotte), иначе рокайль (rocaille), скала (Rocher). В истории искусства ему часто придают неправильный смысл чего-то причудливого, странного, что объясняется иным смыслом того же термина в несколько иной его транскрипции с двойным «t» (Grotesque вместо Grottesque).
** «Singerie» —термин, обозначающий декоративные украшения в духе эпохи Людовика XV.
Как-то я был приглашен к Андре Жаулю на обед с Джоном Дейлом, президентом нью-йорской фирмы «Чарльз Харди». Джон Дейл брался наладить массовое производство Модулора, так как считал его столь же необходимым инструментом на чертежном столе, как и циркуль. Когда я изложил ему принцип построения Модулора, он сказал: «Я все прекрасно понял, ибо каждый вечер играю дома на виолончели, причем мои пальцы перемещаются по струнам, подчиняясь математическим закономерностям, увязанным с человеческим масштабом».
Модулор — мерило, основанное на сочетании математики и человеческого масштаба; оно состоит из двух рядов числовых величин — красного ряда и синего ряда. Можно ли ограничиться одной только числовой таблицей? Нет. И мне вновь хочется пояснить весь комплекс идей, положенных в основу изобретения.
Метр — это всего только условная, абстрактная вели чина; сантиметр, дециметр, метр — это всего только наименования, принятые в десятичной системе. Ниже я выскажу свое мнение о миллиметре. Числовые величины модулора — это размеры конкретные, обладающие материальностью: они представляют собой результат выбора из бесконечного множества величин. Эти меры — величины числовые и обладают всеми свойствами чисел. Сооружения, размеры которых должны быть назначены с их помощью, — это либо предназначенные для человека пространства, либо различные приспособления. Для того чтобы выбрать оптимальные размеры, лучше всего их видеть, оценить ощупывая руками, а не только принять их умозрительно (это, конечно, относится к размерам. близким к размерам человеческой фигуры). Поэтому мерная линия Модулора, которую можно развернуть руками, должна всегда находиться на чертежном столе наряду с циркулем; с ее помощью можно зрительно сопоставить размеры и сделать конкретный выбор.
Открыв закономерности Модулора, надо было найти метод их использования, а следовательно, решить вопрос практического оформления Модулора. Джон Дейл поручил руководство этими чисто техническими исследованиями архитектору Стамо Пападаки. Ему следовало решить, какой же конкретный вид будет придан Модулору и какая отрасль промышленности будет его изготовлять.
Было предложено три варианта.
I. Лента из металла или пластмассы длиной 2,26 м (89 дюймов).
II. Таблица с рядами практически нужных числовых величин. Под «практически нужными» подразумеваются пределы практически применяемых размеров. Они определяются возможностью их восприятия, зрительного и чувственного. Мы считаем, например, что размеры, превышающие 400 м, не могут быть зрительно оценены, да и в этом нет практической необходимости, даже когда речь идет о градостроительстве. Мы стремимся избежать необоснованно гипертрофированных размеров городов, подобных идеям некоторых военных городов эпохи Возрождения; они не воспринимаются ни зрительно, ни умозрительно: это породило в градостроительстве чисто теоретическое направление и привело к созданию оторванных от реальной жизни проектов городов, которые не смогли бы быть восприняты. Это направление было неизбежно бесплодным и должно было стать гибель¬ным для архитектуры; оно свело градостроительство к изображению на чертежных досках городов в виде звезды, квадрата или других совершенных, но явно надуманных форм.
III. Буклет, разъясняющий принципы построения Модулора и возможность на этой основе создать большое разнообразие сочетаний.
Достоинства Модулора, если он вообще имеет право на существование, проявятся при использовании его для назначения размеров изделий промышленного производства. Джон Дейл имеет в виду завершить дело изданием бюллетеня о Модулоре, где будут помещены отзывы о нем специалистов.
В качестве одного из десяти экспертов Объединенных Наций я приступил 28 января 1947 года к разработке проекта комплекса зданий штаб-квартиры ООН на Ист-Ривер в Нью-Йорке. Не знаю, каким образом, но здесь уже знали о Модулоре. Меня попросили сделать доклад на конгрессе Общества американских дизайнеров, проходившем в большой аудитории Метрополитен-Музеум.
Несколько месяцев спустя педагогический состав и студенты архитектурного института в Колумбии, а также министр национального просвещения оказали мне в Боготе исключительно сердечный прием и заявили, что возлагают на Модулор большие надежды. В сентябре того же года такой же интерес был проявлен со стороны VI конгресса CIAM, состоявшегося в Бриджуотере (Англия). Лондонский журнал «Architectural Review» посвятил изложению основных принципов Модулора целый номер, иллюстрированный пояснительными схемами. Одним из авторов этого номера был Матила Гика, как будто давший ответ на вопрос, который я себе задаю каждый день: если Модулор прокладывает путь к чудесным свойствам чисел, направлен ли он только по одному, случайно подвернувшемуся пути из множества других, существующих или могущих быть, или же по счастливому случаю найден именно тот путь, который нужен? Гика, судя по тому, что он пишет, склонен признать второе. Как я уже говорил, этот вопрос не выходит у меня из головы, он всегда преследует меня. Я постоянно задаю его своим собеседникам. Но какой бы ответ мне ни давали, я сохраняю за собой право сомневаться в бесспорности решений, принятых на основе Модулора, я сохраняю полную свободу действий, которая всегда будет определяться моим чутьем вещей, но отнюдь не только разумом.
По возвращении из Америки в июле 1947 года я пен лучил возможность, после годичного перерыва, непосредственно руководить своей мастерской. В кропотливой работе, связанной со строительством в Марселе, Сен-Дье, Байи и других местах, Модулор был проверен на деле. Оценка оказалась настолько положительной, что мне представляется необходимым показать читателям всю механику пользования Модулором.
 |
Нужно сказать еще несколько слов о втором варианте Модулора, в основу которого положен шестифутовый рост человека. Он объясняется весьма простыми соображениями: предметы, размеры которых назначены по Модулору, рассчитаны на распространение по всему свету, и они могут оказаться в распоряжении потребителей, принадлежащих к разным расам, отличающимся ростом, естественно поэтому ориентироваться на людей высоких (шесть футов). Это приведет к назначению во всех архитектурных сооружениях размеров по наибольшему пределу. Помещения, размеры которых назначены на этой основе, смогут быть использованы всеми.
В августе 1948 года при подготовке этой книги к изданию меня вновь взяло сомнение по поводу первой принципа, положенного в основу идеи Модулора, по поводу определения положения третьего квадрата вписанного в два смежных квадрата путем построения, названного «правилом вписанного прямого угла». Я вновь начертил последовательные схемы построения (рис. 17 и 18) и задумался над значением точек m и n, соединение которых определяет положение наклонной прямой. Касательная к окружности, которую вписывается построенный прямой угол (рис. 18), также наклонная. Меня заинтересовал вопрос: пересекутся ли касательная к окружности наклонная прямая m—n с продолжением основания смежных квадратов g—i и можно ли будет вписать серию убывающих по размерам подобных прямой угольных треугольников, подтверждающих принцип убывающих чисел ряда Фибоначчи с отношением Ø. Повторение в конце краткого исторического обзора уже сказанного, не злоупотребляя терпением читателя, не бесполезно.
 |
 |
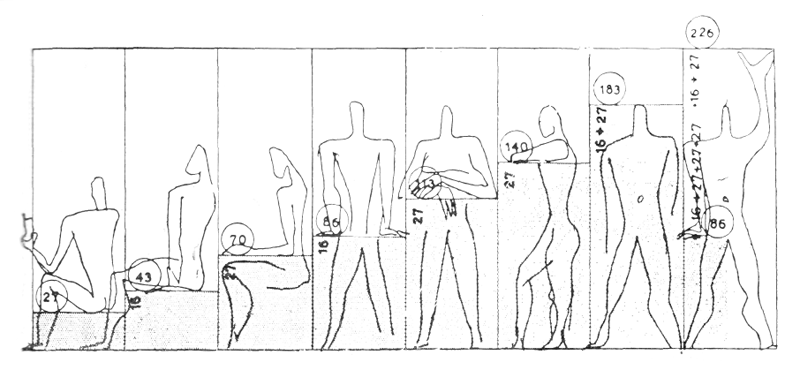 |
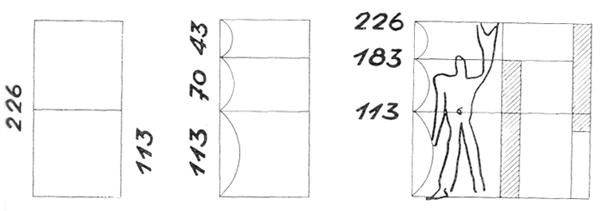
1. В моей пропорциональной сетке приведены три основных размера — 113; 70; 43 (в см.); они находятся в отношениях Ø (золотого сечения) и отвечают ряду Фибоначчи: 43 + 70=113, или 113 — 70 = 43. Их суммирование дает новые числовые величины: 113 + 70=183; 113 + 70 + 43 = 226.
2. Последние три размера — 113, 183, 226 — определяют размеры пространства, в которое вписывается фигура человека ростом в 6 футов.
3. На размерной величине 113 основана величина 70, находящаяся в отношении золотого сечения, которая кладет начало так называемому красному ряду: 4—6—10—16—27—43—70—113—183—296 и т. д.
Мне представляется, что эмблема Модулора может быть дополнена. До сих пор эмблемой фиксировались три, а не четыре основные размерные величины Модулора:
113 — солнечное сплетение;
183 — верхняя точка головы (отношение Ø, 113); 226 — конец пальцев поднятой руки. Другое соотношение, составляющее 140—86, определяет четвертую существенную точку человеческой фигуры — точку опоры опущенной руки — 86 см. Таким образом, человек с поднятой левой рукой, прятавший правую руку за спиной, теперь может ее высвободить и опереться на нее на высоте 86 см. Таким путем будут выявлены четыре основные точки человеческой фигуры, определяющие ее положение в пространстве.
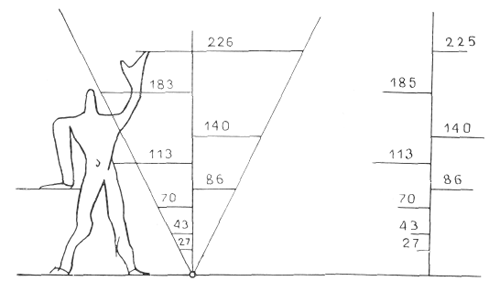
Удвоенный размер 226 (2 x 113) при делении в отношении золотого сечения определяет размерные величины 140 и 86, которые дают начало синему ряду: 13—20,3—33—53—86—140—226—366—592 ...
4. У некоторых из этих размерных величин можно обнаружить связь с положением характерных точек человеческой фигуры (см. рис. 19, 20 и 21).
5. В конечном счете самым важным является неизменная пропорциональность величин, позволяющая получать бесконечное число различных сочетаний, что будет наглядно показано на нескольких таблицах, приведенных во второй части книги, посвященной применению Модулора на практике. Итак, двадцать лет спустя, после выхода в свет книги Матилы Гика «Эстетика пропорций в природе и искусстве» (1927), подтверждены установленные им триада (солнечное сплетение, макушка головы, конец пальцев поднятой руки) и пара (солнечное сплетение и конец пальцев). Они легли в основу красного и синего рядов Модулора, которые могут развиваться безгранично.



Добавить комментарий