Архитектурная рациональность зиждется на экономическом принципе так же, как и техническая рациональность. Разница заключается в том, что техническая рациональность есть экономия труда и материала при создании целесообразного сооружения, а архитектурная рациональность есть экономия психической энергии при восприятии пространственных и функциональных свойств сооружения. Синтез этих двух рациональностей в одном сооружении и есть рациоархитектура. 

 

 

1. При восприятии материальной формы как таковой мы одновременно можем усмотреть в ней выразительность качеств:

1) геометрических — отношения  сторон, ребер, углов, характер поверхностей и т. д.,

2) физических — весомость, плотность, масса и т. д.,

3) физико-механических — устойчивость, подвижность,

4) логических—выразительности поверхности как таковой и ограничивающей объем.

 

В зависимости от выразительности, величины и количества мы можем говорить о:

 

а) мощи и слабости,

б) величии и низменности,

в) конечности и бесконечности.

 

2. Архитектура оперирует этими «качествами» как определенными величинами. Архитектор конструирует форму, внося элементы, которые не являются техническими или утилитарными в обычном смысле слова и которые можно рассматривать как «архитектурные мотивы». В архитектурном отношении эти «мотивы» должны быть рациональны и служить высшей технической потребности человека ориентироваться в пространстве...

 

Для иллюстрации одного из видов работы над геометрической выразительностью формы рассмотрим:

 

Пример 1.

 

3. Две проекции параллелепипеда дают о нем точное геометрическое представление-образ (черт. № 1).

 

 

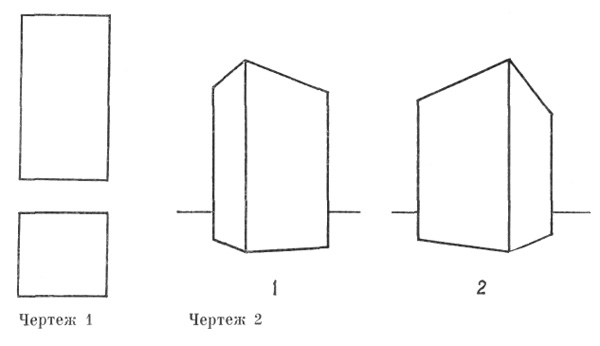
Реальная перспектива ею, представленная в ряде статических моментов 1, 2... (черт. № 2) дает приближенный образ, стремящийся к геометрическому, выраженному в двух проекциях, как к своему пределу.

 

4. Работа архитектора над геометрической выразительностью формы, которую мы всегда воспринимаем в перспективе, заключается в приближении образа, получаемого от восприятия реальной перспективы, к образу, данному в проекциях.

 

Степень приближения зависит от количества и качества входящих в конструируемую архитектором систему определения элементов-признаков. Материалом этой системы элементов-признаков обычно служит в сооружении видимая техническая конструкция. Там, где она может быть использована полностью, создается синтез техники и архитектуры, где этого нельзя, там архитектурная конструкция (элементы-признаки) создается рельефными членениями поверхности формы как наиболее технически простым и экономичным средством исполнения. Конкретным примером постановки и решения задач такого рода могут служить задания, данные мною впервые в 1920 г. на архфаке Вхутемаса.

 

Задание № 1 (форма архитектурно-геометрическая)

 

5. Дано:

 

1) Правильный параллелепипед, в горизонтальной проекции представляющий квадрат 20X20 м, высота 30 м.

2) Высота глаз зрителя 1,60 м, расстояние точки зрения не более 30 м, точка зрения подвижна, скорость не более 15 ж в сек.

3) Освещение солнечное.

 

Примечание. При решении задания необходимо принять во внимание движение солнца и возможность такого его положения, при котором одновременно могут быть равномерно освещены две стороны параллелепипеда.

 

Требуется  показать  зрителю:

 

1) Направление   поверхностей,   образующих   стороны   параллелепипеда, по отношению к координатным плоскостям  (пространственную ориентацию).

 

Примечание. Пространственные координаты те же, что приняты в теории перспективы.

 

2) Ясную читку ребер

3) Равенство сторон

4) Отношение стороны основания к высоте

5) Правильность поверхностей, образующих стороны

6) Прямизну углов (т. е. что углы равны 90°).

 

Средствами выражения могут быть: вертикальные и горизонтальные членения, светотень и фактура поверхностей. 

Требуется  представить:

 

1) Модель или перспективный вид

2) Чертежи 2-х фасадов, образующих взаимно угол

3) Разрез горизонтальный и вертикальный.  Масштаб 1: 100

 

20/Х — 1920 г. Н. Л.

 

6. Как видно из задания, основной работой в нем является выявление для зрителя геометрических качеств параллелепипеда. Но что означает выявить геометрический образ? Разве в математически правильно построенном параллелепипеде мы увидим какую-либо иную форму — шар, конус, цилиндр и т. п.? Нет, мы в нем не увидим ни шара, ни цилиндра и т. д., но мы также не увидим параллелепипеда с теми геометрическими качествами, которые даны в задании.

 

Достаточно взглянуть на перспективный ряд 1, 2... (черт. № 2), чтобы убедиться в недостаточности признаков, по которым можно было бы определить: что стороны основания равны, что отношение высоты к стороне основания = 1,5 :1.

 

Можно ли допустить, чтобы архитектор, строя форму, не знал, как ее будет воспринимать зритель? Такое допущение означало бы полную беспринципность и невозможность какого бы то ни было мастерства в области геометрической выразительности. Необходимо установить положение, что архитектурно-геометрическая сторона материальной формы заключается в такой ее проработке, при которой зритель действительно видит ее геометрическую характеристику в той мере, в которой это необходимо для данною случая.

 

Что для этого нужно сделать в данном примере?

 

7. Необходимо поставить знак тождества между каждой парой одновременно видимых сторон параллелепипеда, следовательно, между всеми сторонами его.

 

Это означает, что членения на поверхности всех сторон параллелепипеда должны быть тождественны (1)

 

 

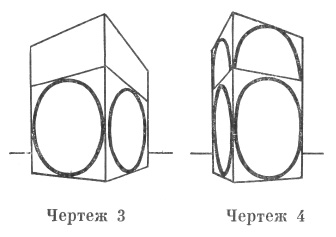
Если для примера мы впишем по окружности на каждую из сторон параллелепипеда так (черт. № 3), чтобы зритель мог при восприятии определить равенство диаметров каждой пары одновременно видимых окружностей, то этим будет дана некая степень приближения образа к его геометрической сущности, будет более уяснено равенство расстояний отдельных ребер от переднего ребра (2)

 

Вписав еще по полокружности (черт. № 4), мы уясним отношение основания к высоте 1:172, равенство сторон и все вытекающие следствия, все в известной степени приближения, какое могут дать эти элементы (3)

 

Продолжая таким образом анализ, далее мы найдем и остальные Элементы, необходимые для решения задания.

 

Сравнивая архитектурные образы, полученные в результате такой обработки, с перспективным рядом 1, 2... (черт. № 2), при тех же условиях зрения, можно убедиться в большой степени приближения образа архитектурного (черт. № 4) к образу, данному в проекциях (черт. № 1).

 

 

Действие света на моделировку общепонятно. В данном задании поставлено определенное требование § 3. Решение возможно:

 

а) или различной фактурной обработкой каждой пары одновременно видимых поверхностей (4),

б) или   расчленением   одной из каждых двух одновременно видимых поверхностей на  участки, составляющие   угол к поверхности, часть которой они составляют (5),

в) или расчленением обеих одновременно видимых поверхностей, как в п. 5, но углы частных поверхностей одной стороны не равны углам частных поверхностей другой (6)

 

Пример решения

 

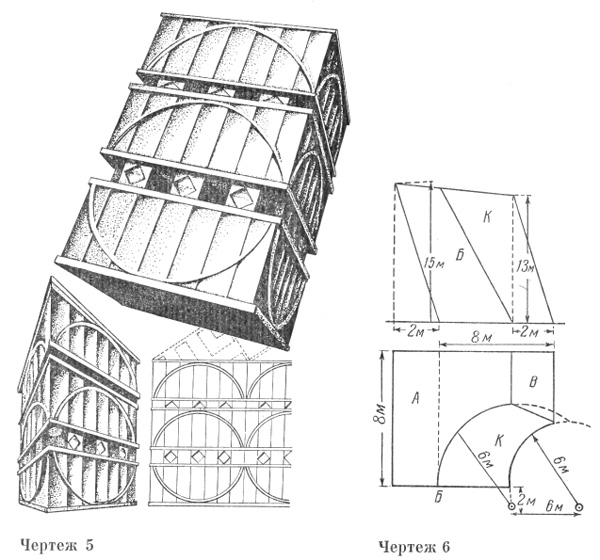
8. В приведенном решении Петрова § 1, 2, 5, 6 задания выявлены следующими средствами:

 

§ 1 и 2 двухкратным повторением горизонтальных проекций параллелепипеда,

 

§ 5 прямолинейными вертикальными и горизонтальными, взаимно перпендикулярными членениями поверхностей, § 6 показанием в углах горизонтальных проекций, видимых снизу небольших квадратов, которые оцениваются как таковые непосредственно в силу малой величины их, для усиления в них вписаны малые окружности.

 

Задание № 2 (форма архитектурно-геометрическая)

 

9. Дано:

1) Прилагаемый чертеж геометрической формы [черт. № 6]

2) Горизонт зрения нормальный, точка зрения подвижна, скорость не более 15 м, максимальное расстояние точки зрения 30 м.

3) Освещение солнечное

 

Требуется показать зрителю:

1) Все плоскости как таковые

2) Плоскости А и Б как образующие угол

3) Наклонность плоскости В

4) Цилиндричность или конусовидность поверхности К

5) Ясную читку всех углов

 

Необходимо представить:

 

Макет и чертежи в М 1:100

Вхутемас 30/Х — 1920 г. Н. Л.