Материалов и сообщений становится все больше. Слово предоставляется теперь тем, кто применял Модулор

 

В воздухе все время носился волнующий вопрос: «как и зачем?» 25 октября 1948 г. я направил г-же Майяр вопросник в расчете на то, что она с помощью друзей в Сорбонне сумеет дать мне ответ. 

 

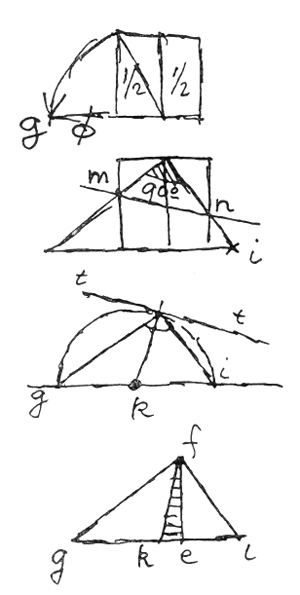
На рис. 60—1 показано построение, которое определяет точку g.

 

60—2 — положение вершины вписанного угла, это построение определяет точки i, m и n.

60—3 — вписанный в окружность прямой угол определяет положение наклонной касательной t — t'; делится в точке k пополам.

60—4 — получаем треугольник kfe;

еf — вертикальная ось исходного квадрата;

kf — радиус окружности.

 

 

Вопрос I — каково отношение kf k ef?

kf k eg и kei?

 

Вопрос II — касательная в точке f и наклонная прямая mn, каково отношение между ними? Их направление? Пересекаются ли они и в какой точке? 

 

Математик Татон ответил так:

 

Париж, 5 ноября 1948 г.

«Мсье, сообщаю   Вам  ответы на поставленные вопросы. Выводы даны на отпечатанном на  машинке листе, расчеты приложены на отдельном листе. Надеюсь, что ответы Вас удовлетворят. Я  всегда к Вашим услугам и готов дать дополнительные разъяснения и ответить на новые вопросы. Очень рад случаю познакомиться с Вами. Примите наилучшее пожелание

Уважающий Вас Р. Татон»

 

Привожу его выводы:

 

«1. Принимаем за единицу сторону исходного квадрата gk = ki = 1,006 (считая, что gi делится в точке А: пополам и является центром окружности, проведенной через точки g, i и f, в которую вписан прямой угол §7'г).

Следовательно, квадраты, построенные на gk и ki, зрительно кажутся квадратами, а строго математически — это близкие к квадрату прямоугольники.

2. Отношение kf : ei = 1,006 : 0,8944 = 1,1125. Касательная в точке f  и  наклонная mn — параллельны: они образуют с горизонталью угол 6°19'. Обе они перпендикулярны к радиусу kf. Касательная пересекает продолжение горизонтального основания на расстоянии 8,94 вправо от точки е.

3. Рассматривая последовательно уменьшающиеся треугольники, полученные в процессе развития построения, видно, что точка p' относится только к касательной, проведенной в точке f.

 

Прямые линии mn в последовательно уменьшающихся треугольниках параллельны друг другу и касательной; продолжение отрезка mn первого треугольника пересекает линию основания в p", причем Е р" = 4,44; последующие прямые треугольников пересекают линию основания в точках, стремящихся к точке р'.

 

Примечание. Последовательный ряд треугольников непрерывно стремится к точке р', однако ее не достигнет, поскольку в каждом последующем треугольнике мы возвращаемся к исходной фигуре, лишь в уменьшенном масштабе.

 

Каждый последующий треугольник составляет по размерам 4/5 предыдущего.

Р. Татон

 

Ответ математика может быть истолкован следующим образом: исходная гипотеза 1942 года получила подтверждение: «Берем два одинаковых смежных квадрата и с помощью вписанного прямого угла определяем    положение    третьего,   равновеликого   квадрата».  

Однако...

 

Однако математик говорит: ваши исходные квадраты не являются квадратами; одна из сторон больше другой на шесть тысячных...

 

На практике, в повседневной жизни, величина в шесть тысячных относится к тем, которыми пренебрегают и которые не учитывают; она зрительно не воспринимается.

 

Но в философии (для меня эта суровая наука недоступна) эти шесть тысячных, я чую, имеют исключительно важное значение; вопрос остается открытым повеяло свежим воздухом — это сама жизнь, предоставляющая неизбежное, но отнюдь не тождественное, повторение пройденного — это и порождает продвижение.

 

 

•

 

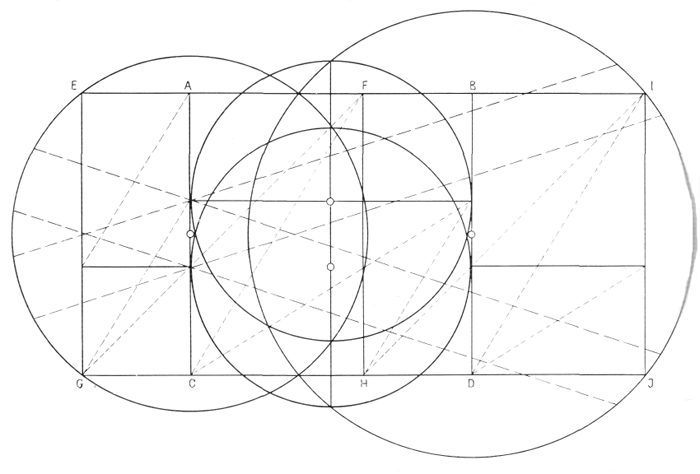
4 декабря 1948 г. г-жа Э. Майяр прислала мне ответ в виде выполненного с помощью циркуля чертежа, а заметкой, написанной карандашом: «три квадрата, четыре окружности..,  диагонали других членений, частично квадратных, частично   прямоугольных, со сторонами в отношении золотого сечения; диагонали, определяющие положение малых окружностей, выведены за пределы этих окружностей».

 

•

 

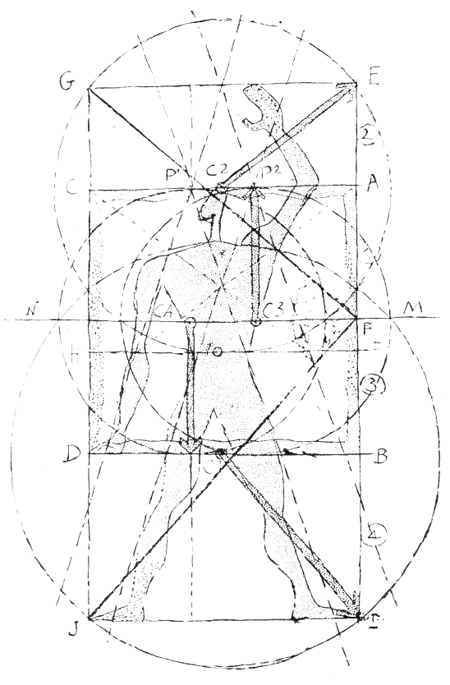
12 декабря 1948 г. я поставил рисунок г-жи Майям вертикально и вписал в него фигуру человека с поднятой рукой (в цвете). Я возвратил главную роль в чертеже прямоугольникам и квадратам. Я сделал на нем надпись:

Этим рисунком, подтверждающим первоначальную гипотезу, я завершаю свое исследование Модулора.  Могу только добавить: «Это божественная игра», и я наблюдаю за ней, благоразумно стоя за оградой этого чудесного сада.

 

Конец

 

С конца 1948 г. и по сегодняшний день, 23 сентября 1949 г., когда книга подписана в печать, вокруг Модулора происходит какое-то брожение.

 

Идея Модулора   постепенно   проникала,   просачивалась и дошла до видных деятелей Европы и Америки, вызывая интерес, сомнения, вопросы, замечания.

 

•

 

Посмотрим, что будет дальше! Мне известно, что те, кто притронулся к этому хорошо настроенному инструменту, уже с ним не расстается.

 

Слово за всеми, кто попробует и применит, кто будет настойчив, будет спорить, вносить поправки и предложения.

 

Еще в 1946 г. я говорил Джону Дейлу: «Я отказался от реализации патента. Я придерживаюсь того, чтобы мерная лента Модулора в качестве рабочего инструмента изготовлялась в США; она займет свое место на чертежном столе рядом с циркулем. Следовало бы основать общество друзей Модулора, всемирное содружество тех, кто в него верит. Для распространения идей Модулора должен издаваться международный журнал на различных языках мира и, кроме того, на искусственно созданном языке, без которого скоро не обойтись; в журнале смогут обмениваться мнениями создатели Модулора и пользующиеся им, в целях внесения более крупных или мелких совершенствований. Какие материалы будет публиковать этот всемирный журнал?

 

От высшей математики до самых скромных проявлений повседневной жизни, включая внешнюю среду и предметы обихода и широкого потребления, от оборудования кухонь до «храмов Будущего» для мира, стремящегося к объединению.

 

Отныне слово за теми, кто пользуется в своей работе Модулором.