Проверка на конкретных примерах
Изобретатель интуитивно обращает внимание на то что может подтвердить его открытие, и мимо чем другой бы прошел, не заметив. Привожу этому не сколько доказательств.
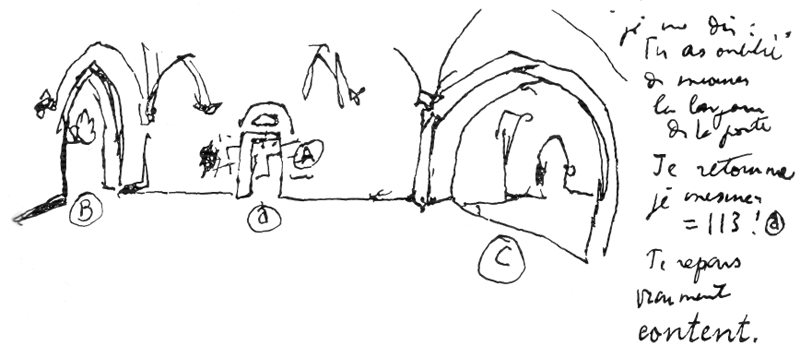
Монастырь Шаалис (близ Парижа). Прошлым летом, 1948 года, я задержался перед руинами этого цистерианского монастыря XIII века. Меня поразив великолепные пропорции входных дверей (насколько помню, ведущих в трансепт).
Я достал из кармана Модулор: высота проема А равна точно 226. Ширина проема В — 226! Ширим проема С — 336 = 226 + 140! Я пошел дальше удовлетворенный. Пройдя 200 метров, я остановился и задумался, вспомнив, что забыл промерить ширину проема А. Вернулся, измерил ширину d — она оказалась равной 113! Все это объяснялось тем, что создатели монастыря пользовались отношениями золотого сечения. Исходным размером был рост человека в 1,82 м = 6 ф. Теперь я получил полное удовлетворение.
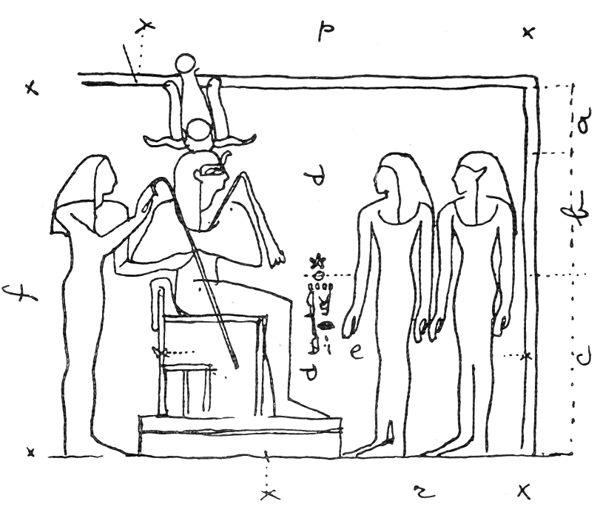
Египет. Осенью 1948 года я задумался над изяществом, строгостью и совершенством египетского искусства. Я открыл книгу Гюстава Лебона «Древние цивилизации» на стр. 425 с фотографией барельефа храме фараона Сети I в Абидосе. Мне показалось, что принятые в нем размеры соответствуют числам ряда Фибоначчи, построенного на основе размеров человеческой фигуры. На рис. 52 приведены размеры в миллиметрах, измеренные по фотографии; весьма примечательны их соотношения: размеры a, b и c относятся к ряду Фибоначчи с отношением Ø. Размерные вели чины d и а определяют положение небольшого диска в центре надписи иероглифами. Этот маленький диск сразу привлек мое внимание. Помимо этого размерная величина d + α повторена в размерам обозначенных f и e.
3 октября 1948 года я прилетел в Стамбул. На следующий день я был принят профессором Уайтмором в соборе Святой Софии, где группа молодых археологов под его руководством пыталась открыть мо заики, веками скрытые под позднейшими записями Мы находились в галерее, в месте, отмеченном большим диском черного мрамора, утопленным в полу г балюстрады галереи, выходящей в неф. Это место императора Юстиниана. Меня заинтересовала балюстрада из великолепного скульптурно обработанного мрамора. Измеряю высоту балюстрады Модулором. Точно 113 см.
Часом позже мы были в самом сердце древней Византии — в соборе Кахриэ, известном своей мозаикой, сохранившейся в течение сотен лет; ее почитали даже турки. Мне показалась крайне удачной принятая ширина нартекса. Я промерил ширину Модулором; она оказалась равной 226 + 113 = 339. В следующую субботу, по возвращении из Измира, я вновь остановился в Стамбуле. На этот раз мое внимание было привлечено входным дверным проемом в Большом Серале (он ведет на холм, окруженный некогда неприступными стенами, укрывавшими султанов и их гаремы, с восхитительными киосками, чудесными растениями, с видом на сказочный пейзаж, охватывающий устье Босфора, Мраморное море и Золотой Рог).
Размеры дверного проема: 226 + 70 = 296 (все три размера Модулора). Ширина боковой ниши 2,23 м.
Общежитие швейцарских студентов в университетском городке в Париже 1930—1932 гг. При постройке этого здания мне пришлось подчиниться строгим, хотя и необоснованным требованиям действующих строительных правил.
 |
 |
 |
 |
 |
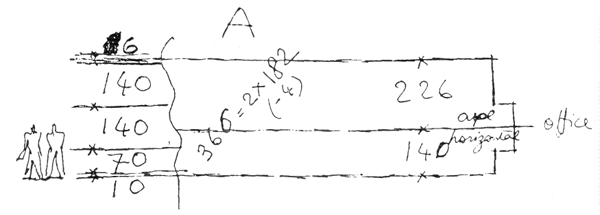
В настенной живописи, выполненной мною в сентябре 1948 года на криволинейной в плане стене библиотеки, я остановился на соотношении размеров, возникшем по интуиции без предварительных расчетов: 140 + 226. Итого 366 (близко к размеру 2 х 180).
Облицовывая эту изогнутую стену плитами изореля на раскладках, можно было использовать плиты размером по высоте 140 + 140 + 70; образовавшиеся зазоры создали тонкие полоски у основания живописи, у пола и наверху, у потолка. При переносе эскиза на стену оказалось, что принятые размеры отвечают Модулору.
Грузовые суда. Моим соседом в самолете, на которое я летел из Измира в Стамбул, был молодой турок—инженер торгового пароходства. «Я еду в Гетеборг, чтобы принять новое грузовое судно», — сказал он мне. «Можете ли сказать, — спросил я его, — какая принята высота между палубами в чистоте?» «Высота в чистоте между палубами равна 2,26 м».— «Можете ли вы показать это на чертеже?» — «Пожалуйста. Могу кстати добавить, что и в пассажирских судах пассажирские каюты делаются такой же высоты».
В стремлении к уюту и экономичности общего решения судостроители пошли по пути архитекторов XVIII века, добивавшихся по настоянию дам интимности и комфорта в созданном ими типе «Малых апартаментов».
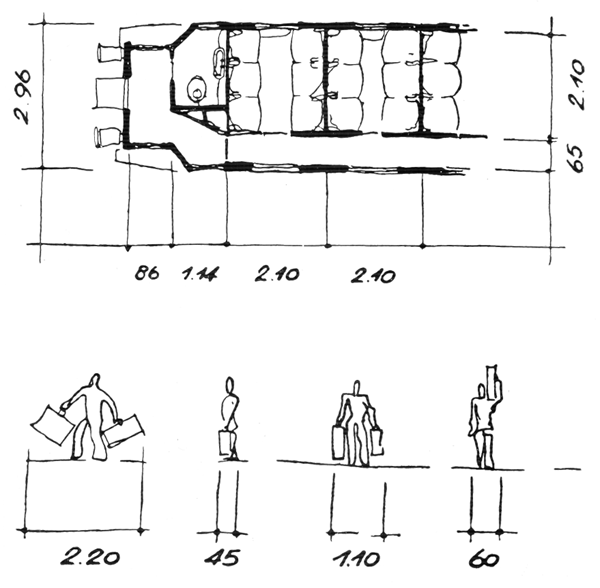
Железнодорожные вагоны. Купе — своего рода емкости для людей, с размерами, отвечающими человеческому масштабу.
Размеры купе льют воду на мою мельницу (рис. 56).
Парфенон. Октябрь 1948 года. Совершенно случайно в мои руки попали исключительно интересные материалы. То были копии обмерных чертежей, составленных в 1923—1931 гг. Баланосом; в них приведены точные размеры каждого из мраморных блоков, использованных во всех частях Парфенона — в ступенях, колоннах, в антаблементе.
На основании изучения этих размеров можно прийти к тысячам выводов. При первом же просмотре этих числовых величин, приведенных на двадцати с лишним листах больших размеров, я решил сопоставить их с размерами по Модулору (в основу которого взят рост человека в 175 см, 108—216); ведь греки были, без сомнения, менее рослыми, чем англосаксы или скандинавы. В этих условиях знакомство с упомянутыми числовыми величинами оказалось достаточно обнадеживающим.., учитывая мою убежденность и внесение поправок на доли дюйма или миллиметра!!! По своему совершенству Парфенон — памятник исключительный, с бесконечным богатством в нюансах.
Это не просто построенное здание, а подлинное произведение скульптуры. В нем использовано множество «оптических поправок», учитывающих его расположение на краю холма Акрополя и интенсивность солнечного света в Греции.
Иктин, Калликрат и Фидий сыграли с нами неплохую шутку; при измерении размеров колонн мы убеждаемся, что их высота точно равна 10 метрам (* По данным обмеров, высота колонны составляет 10,43 м.); можно подумать, что они предвосхитили систему мер, установленную Национальным конвентом в 1793 году!!!
Я еще раз повторяю: Парфенон — грандиозная скульптура, вписанная в прекрасный ландшафт Гиметта, Пентеликона, Пирея и островов. Это сооружение не подчинено определенным соотношениям числовых величин, как, например, соборы (в сводах и аркбутанах) и даже Эйфелева башня и жилой дом в Марселе (пример структуры, основанной на пропорциональности размеров).
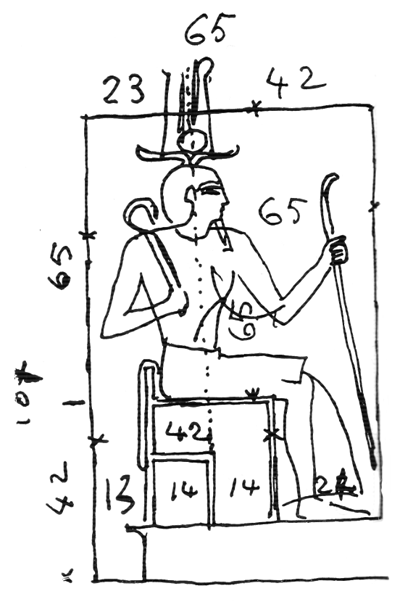
Фараон. Сидящая фигура Рамзеса подтверждает существование графических методов построения композиции (рис. 55). Размеры, показанные на рисунке, соответствуют размерам в мм на чертеже Шампольона в книге Гюстава Лебона «Древние цивилизации». Читатель может убедиться в существовании между ними определенных математических соотношений.
 |
 |
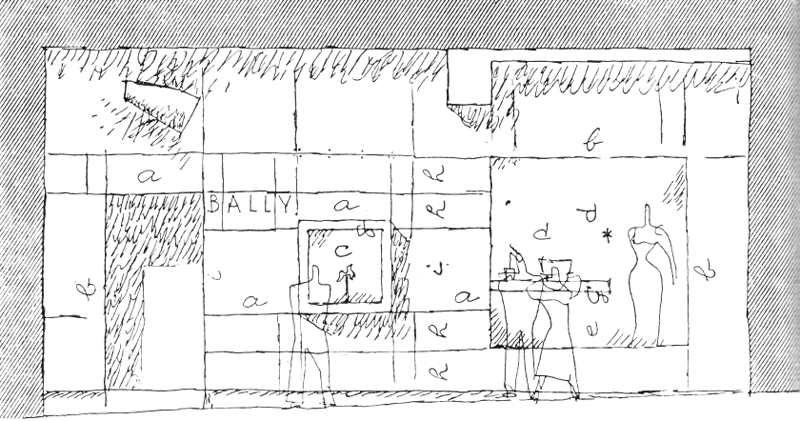 |
Проект фасада магазина Байи на бульваре Мадлен в Париже, 1948 год. Фасад решен в виде металлической облицовки с тремя проемами. Композиция, безусловно, производит впечатление большого разнообразия.
а = 113 — к. р.;
b = 226 — с. р.;
с = 86,3 — с.р.;
g = ½ от 26,6 — к.р.= 13,3;
d = 140 — с. р.;
l = 86 — g(13) с. р. = 73;
h = 43 — к.р.;
i = 113 — g(13) с. р.= 100.
Использование в качестве основы композиции графического метода построения может быть и в начале, и в середине, и в конце пути к созданию прекрасного. Когда же зарождается идея? (выражаясь на профессиональном жаргоне — когда осеняет вдохновение?). До того, как художник взял в руки карандаш, или уже во время работы? Вопрос решается по-разному, в зависимости от обстоятельств, от самой работы, от характера и даже просто от самочувствия. Для подлинного искусства правил не существует: оно может одержать победу или потерпеть поражение в зависимости от предложенных решений, от столкновений идей, от эмоций, от материальных возможностей и т. д. Произведение искусства знаменует собой материализованное воплощение бесконечной и трудно выражаемой внутренней борьбы художника. Математический расчет является таким же элементом творчества, как цвет, как величина, рисунок, пространство и т. п. Я настаиваю на праве искусства быть разнообразным. Я признаю за искусством обязанность быть новаторским, невиданным, неповторимым. Я требую от искусства, чтобы оно было способно вызвать игру мыслей. Серна, совершая огромный прыжок с одной скалы на другую, передает вес всего своего тела на копыто, укрепленное в щиколотке, диаметром всего 2 см — это в полном смысле вызов, но вызов, обоснованный математическим расчетом. Чудеса математики неизменно развиваются от простейшей арифметики (столь полезной в повседневной жизни) к божественной игре чисел, происходящей где-то там, за стеной. Когда мы воскрешаем в памяти вспышки прозрения глубочайших истин, которые удалось неожиданно постичь на случайном перекрестке путей, нет необходимости предаваться восторгам и экстазу. Слова остаются словами: мы ими обозначаем веши.
Но существуют вещи, в которых разбираются далеко) не все. Однако гармония воспринимается всеми. В этой работе идет речь об инструменте, именуемом Модулором, лежащем на чертежном столе рядом с: карандашом, рейсшиной и угольником. Разве рейсшина и угольник являются преступным нарушением здравого смысла и творческого воображения? Спорой по этому вопросу быть не может.
Геометрическое мышление может привести к созданию блестящих чертежей.
Архитектуру, основанную на треугольнике, в эпоху Возрождения называли «аллагерманика».
Для вычерчивания квадрата циркуль не требуется: архитектура, основанная на квадрате, оперирует или плоскостями, или простейшими призмами, ограниченными квадратами или прямоугольниками, что позволяет с легкостью и объективно определить их соотношения.



Добавить комментарий